4. Lektion: Das Centmaß für Intervalle: Joachim Mohr Mathematik Musik

Joachim Mohr Mathematik Musik

Lektion 1 Lektion 2 Lektion 3 Lektion 4 Lektion 5 Lektion 6 Lektion 7 Lektion 8 Lektion 9

Kurzfassung: Das Centmaß
Weiter mit Lektion 5 Die gleichstufige Stimmung

4. Lektion: Das Centmaß für Intervalle

Kurzgefasst wird im Folgenden erklärt:

Als Einheit wählen wir die Oktave und ihre Untereinheit Cent. Wir zählen dann die Oktaven, die ein Intervall umfasst:
1 Oktave = 1200 Cent
2 Oktaven = 2400 Cent
3 Oktaven = 3600 Cent
...

Jedes Intervall kann als Vielfaches der Oktav dargestellt werden.
Bekanntermaßen sind angenähert 12 Quinten = 7 Oktaven.
Also ungefähr: Qui=7/12 Ok = 700 Cent (genau 702 Cent. Berechnung folgt später).

Die Oktave wird in 1200 Cent (12 Halbtöne) unterteilt: 1Ok = 1200Cent, 1 Halbton=¹/₁₂Ok = 100 Cent.
Der Zusammenhang Frequenzverhältnis zu Intervall ist ein logarithmischer.

Die Centangabe wird vorteilhaft bei Verstimmungen verwendet. Grob gesagt:

Abweichung bis 10 Cent - wie bei mitteltönigen Stimmungen, bei denen nur C-Dur nahe Akkorde verwendet werden, bringen im Vergleich zur reinen Stimmung Farbe in die Musik.
Mit 15 Cent Abweichung hat man sich schweren Herzens abgefunden. Anders könnte man auf Tasteninstrumenten nicht alle Tonleitern spielen.
Fürchterlich klingen Verstimmungen um die 40 Cent (ein Fünftel eines Ganztones) wie zum Beispiel beim "Wolf" bei der ansonsten so herrlichen mitteltönigen Stimmung, bei Cis-Des oder bei As-Fis.

Die Verwendung des Centmaßes von Intervallen in der Musiktheorie

Intervalle kann man als Vielfache von einer Oktave angeben. Es handelt sich dabei um ein logarithmisches Maß der Frequenzverhältnisse. Cent ist eine Untereinheit der Oktave mit der Definition ''1200 Cent = 1 Oktave'' (oder ''1 gleichstufiger Halbton = 100 Cent''). Hiermit ist ein sehr genauen Vergleich der Intervallgröße möglich. Das Centmaß ist proportional zur Intervallgröße, während das Frequenzverhältnis sich exponentiell verhält.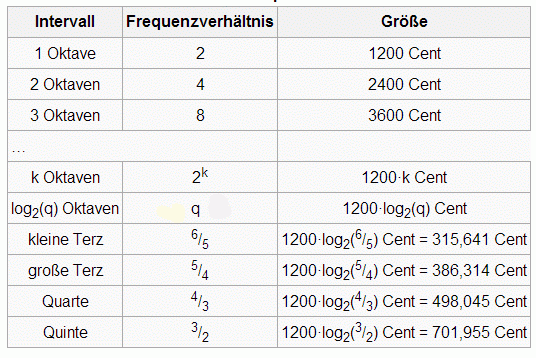
tabelle

Beachte: Löst man die Exponentialgleichung q=2^k nach k auf, so benötigt man den Logarithmus k=log₂(q) zur Basis 2.
Werden Intervalle hintereinander ausgeführt, kann man ihre Größen in Cent addieren (während ihre Frequenzverhältnisse multipliziert werden müssen).

Beispiel:
Quinte + Quarte = 702 Cent + 498 Cent = 1200 Cent = Oktave. (Frequenzverhältnisse: ³/₂·⁴/₃ = ²/₁.)
Kleine Terz + große Terz = 316 Cent + 386 Cent = 702 Cent = Quinte. (Frequenzverhältnisse: ⁶/₅·⁵/₄ = ³/₂.)

Nun Ausführlich:

In unserer Vorstellung haben zwei gleiche Oktaven, allgemein zwei gleiche Intervalle, immer denselben Abstand.

Wir sprechen von 1, 2, 3 Oktaven u.s.w. Die Frequenzverhältnisse sind jedoch 2, 4, 8 u. s. w.

Veranschaulichung der Frequenzverhältnisse im Gegensatz zu unserer Vorstellung:

Maßstab: Frequenzen:

Interpretation:
-1Ok: Eine Oktave tiefer (Frequenzverhältnis 1:2)
0Ok: Prim (Frequenzverhältnis 1:1)
1Ok: Eine Oktave höher (Frequenzverhältnis 2:1)
2Ok: Zwei Oktaven höher (Frequenzverhältnis 4:1)
3Ok: Drei Oktaven höher (Frequenzverhältnis 8:1)

Maßstab: Unser Höreindruck (das Weber-Fechnersche Gesetz):

Mit der Bezeichnung: lb ist der Logarithmus zur Basis 2 und der Feinunterteilung: 1Ok = 1200Cent

Intervall = lb(Frequenzverhältnis)·Ok
y = lb(x)Ok = lb(x)·1200Cent
(Das Intervall y als Teil der Oktave Ok in Abhängigkeit vom Frequenzverhältnis x)
Zum Beispiel ist das Frequenzverhältnis von 3 Okaven x=2·2·2=2³ =8 und damit das Intervall
y=lb(8)Ok=3Ok (muß ja so sein!).

Begründung:lb(8) ist der Zweierlogarithmus von 8, also die Zahl, mit der ich zwei potenzieren muß, um 8 zu erhalten, somit lb(8) = 3. Der Zweierlogarithmus macht das Potenzieren rückgängig.

Allgemein ist der Zweierlogarithmus lb(x) als die Zahl definiert, mit der man zwei potenzieren muß, um x zu erhalten:
y=lb(x) 〈=〉 2^y = x
Der Zweierlogatithmus und die Potenzen zur Basis 2 sind als Funktionen betrachtet Umkehrfunktionen von einander.
Ausführlicher: siehe Einführung in den Logarithmus.

Jedes Intervall wird nun auf die Oktav bezogen mit dem Maß Cent.

Zum Beispiel:

1 Ok = 1 200 Cent
2 Ok = 2 400 Cent
3 Ok = 3 600 Cent
...
Das Frequenzverhältnis von einer, von zwei, von drei, ... Oktaven ist 2,4,8 ...
Mit den Beziehungen 1 = lb(2), 2 = lb(4), 3 = lb(8), ... können wir deshalb auch schreiben:

1 Ok = lb(2)·1200 Cent
2 Ok = lb(4)·1200 Cent
3 Ok = lb(8)·1200 Cent.

Die übrigen Intervalle berechnen sich dann entsprechend:

         3
Qui = lb(-)·1200 Cent = 702 Cent
         2

         4
Qua = lb(-)·1200 Cent = 498 Cent
         3

...

Bemerkung:

In der gleichförmigen Stimmung mit dem Halbton h = 100 Cent gilt:
Qui(gleichstufig) = 7 h = 700 Cent und
Qua(gleichstufig) = 5 h = 500 Cent.

Die feinen Unterschiede zwischen reiner und gleichstufiger Stimmung werden in Lektion 5 erklärt.

Noch ein Beispiel:

gT = lb(5/4)Ok = 0,321 928Ok = 0,321 928·1200 Cent = 386 Cent

Mit gT = 0,321 928Ok wird zum Ausdruck gebracht:
Die große Terz ist das 0,321 928-Vielfache der Oktave.
Grob abgeschätzt: Die große Terz ist ungefähr ein Drittel einer Oktav, da drei große Terzen aufeinandergetürmt ungefähr eine Oktave ergeben.

Da 1 Oktave = 1200 Cent umfaßt, ist mit dem feinen Maß Cent ausgedrückt:
gT = 0,321 928·1200 Cent = 386 Cent (gerundet).

Der große Nachteil ist, dass die Reinheit von Intervallen, deren Frequenzverhältnis einfache Verhältnisse sind, in der Centschreibeweise nicht erkennbar ist, der Vorteil ist ihre gute Vergleichbarkeit.

Bemerkung: In dem Werk "Teilung des Kanons" (siehe 6. Lektion) addiert Euklid die Intervalle Qua+Qui=Ok und bemerkt dazu, dass dies der Multiplikation der Verhältnisse (4:3)·(3:2) = (2:1) entspricht.

Er wußte auch, dass die Qui ungefähr der 7/12-te Teil der Oktave ist (12 Quinten fast gleich 7 Oktaven). Er kannte noch keine Dezimalzahlen (7/12=0,583) und noch keine Logarithmen (lb(3/2)=0,585).

Wenn wir Qua + Qui = 498 Cent + 702 Cent = 1 200 Cent, oder etwas genauer Qua+Qui=498,044 999 135 Cent + 701,955 000 865 Cent = 1 200 Cent, schreiben, wird nicht einmal erkennbar, dass das zugehörige Zahlenverhältnis rational ist.
Die Probe:


 498,044 999 135 Cent     498,044999135/1200
2                     =  2                   = 1,333 333 333

zeigt uns ebenfalls nicht mit absoluter Sicherheit, dass das Verhältnis 4/3, also die Quart, dahinter steckt.

Vom Höhren her ist Qui=lb(3/2)Ok (Interpretation Qui = 0,585-te Teil der Oktave) nicht nachvollziebar, da lb(3/2) irrational ist. Das heißt: Es gibt kein gemeinsames kleineres Intervall, dessen Vielfaches die Oktave und ein anderes Vielfaches die Quinte ist.

Allgemein gilt: Vom Hören her kann man Intervalle nicht beliebig teilen. Ich kann nur feststellen, ob Vielfache eines Intervalls größer als Vielfache eines anderen Intervalls sind und damit Intervalle äußerst genau vergleichen.

Durch die geniale pythagoreische Zuordnung von Intervallen zu Verhältnissen wurde die Vergleichbarkeit mathematisiert.

Auch für uns "moderne" Menschen ist die Aussage Qui = lb(3/2)Ok unwesentlich. Wir können damit allenfalls musikalische Aussagen besser nachrechnen.

Berechnung von Frequenzverhältnissen

Wie kann ich nun umgekehrt aus Intervallen als Teil der Oktave die Frequenzverhältnisse wieder berechnen?

1. Beispiel: Welches Frequenzverhältnis x hat das Intervall y=7 Oktaven?

Lösung: Wir müssen die Gleichung y=lb(x)=7 nach x auflösen.

Erinnern wir uns:

y=lb(x) 〈=〉 2^y = x. Auf unser Beispiel angewandt: 7=lb(x)〈=〉2⁷=x.

Somit gilt für das Frequenzverhältnis x von 7 Oktaven: x = 2⁷=128.

2. Beispiel: Welches Frequenzverhältnis x hat das Intervall y = gT = 0,322Ok?

                           0,322         4
Lösung: lb(x)=0,322 〈=〉 x=2      =1,25 = - 
                                         5

(Frequenzverhältnis der großen Terz). Wir haben hier mit Näherungswerten gerechnet. Die exakte Rechnung lautet:

                          5
                       lb(-)
     5                    4   5
y=lb(-) = lb(x) => x =2     = - .
     4                        4

                    y           lb(x)
Allgemein gilt: lb(2 ) = y und 2     = x.

3. Beispiel Wir wiederholen das 2. Beispiel, diesmal jedoch im Centmaß:

Welches Frequenzverhältnis x hat das Intervall y = gT = 386Cent?

Lösung: Wir müssen zunächst durch 1200 dividieren, da 1Ok = 1200 Cent sind.

                                            386
y=lb(x)Ok=lb(x)·1200Cent=383Cent => lb(x) = ———— = 0,322
                                            1200

                      0,322         5
und damit wieder x = 2     = 1,25 = -
                                    4

Allgemein:

Aus dem Centmaß y = lb(x)·1200 Cent berechnet sich das Frequenzverhältnis über die Umformung

                                y
                            —————————
           y                1200 Cent
lb(x) = ————————   zu x = 2
        1200Cent

Beisspiel:

                         702
                        ————
                        1200
a) y = 702 Cent => x = 2      = 1,500 038

                             3
Ohne Rundungsfehler wäre x = -, 
                             2

also y = reine Quinte.

b) y = 400 Cent (die große Terz bei der gleichstufigen Stimmung)

        400      1
        ————      -
        1200      3
=> x = 2      = 2  = 1,25992 (auf 5 Dezimalen gerundet)

Das Frequenzverhältnis ist irrational, kann also nicht als Bruch angegeben werden.

Musikalische Einführung in den Logarithmus Da das n-fache von Intervallen die n-te Potenz von Frequenzverhältnissen entspricht, kann man "musikalisch" den Logarithmus einführen.
Weiterlesen: Überlegungen zum Zweierlogarithmus für Mathematiker und Informatiker.

Weiter mit ...

Lektion 1 Töne, Intervalle, Frequenzen und Frequenzverhältnisse
Lektion 2 Hintereinanderausführung zweier Tonschritte. Reine Stimmung
Lektion 3 Beschreibung von Tonsystemen ohne Akustik
Lektion 4 Das Centmaß für Intervalle
Lektion 5 Die gleichstufige Stimmung
Lektion 6 Das pythagoreische und syntonische Komma
Lektion 7 Eulersches Tonnetz - Modulationen
Lektion 8 Mitteltönige und wohltemperierte Stimmungen
Lektion 9 Der Akkord der 2. Stufe, die Kommafalle, der neapolitanische Sextakkord und die Doppeldominante