Die Homepage von Joachim Mohr
Lektion 1 Lektion 2 Lektion 3 Lektion 4 Lektion 5 Lektion 6 Lektion 7 Lektion 8 Lektion 9
2. Lektion: Hintereinanderausführung zweier Tonschritte
und
Reine Stimmung
In Lektion 1 wurde dieser Vorgang schon vorweggenommen:"Die Quinte und die Quarte ergänzen sich zur Oktave."
Was bedeutet das?
Nun: Das erste Intervall kann durch zwei Töne A und B beschrieben werden. Das zweite ebenfalls durch zwei Töne, wobei wir als ersten Ton B wählen können. Also:
| Erstes Intervall i1 = AB. In unserem Beispiel etwa Qua = c'f'. | 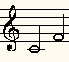 |
Quarte |
| Zweites Intervall i2 = BC. In unserem Beispiel dann Qui = f'c''. | 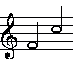 |
Quinte |
Nun führen wir die Intervalle hintereinander aus und lassen den Ton B unberücksicht.
| Neues Intervall i = AC. In unserem Beispiel i = c'c''. | 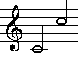 |
Oktav |
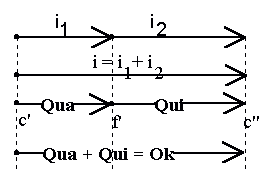
Wir haben also eine "Verknüpfung" von Intervallen, die wir unserer Vorstellung gemäß wie das Zusammensetzen von Strecken vorstellen können und die wir deshalb als Addition schreiben.
i1 = AB und i2 = BC => i = i1 + i 2 = AC.
In unserem Beispiel also Qua + Qui = Okt.
Bei Vielfachen von Intervallen werden die zugehörigen Frequenzverhältnisse potenziert.
Bespiel:
| Quinte | 3/2 |
| 2 Quinten | (3/2)2=9/4 |
| 3 Quinten | (3/2)3=27/8 |
| 4 Quinten | (3/2)2=81/16 |
| ... | |
| 1 Oktave 2 | |
| 2 Oktaven | 22=4 |
| 3 Oktaven | 23=8 |
| 4 Oktaven | 24=16 |
| ... | |
| n Oktaven | 2n |
| 1/12 Oktave |
1 —— 12 12—— 2 = \/ 2 |
Bei der Addition von Intervallen werden die zugehörigen Frequenzverhältnisse multipliziert.
Beispiele:
| G + Qua = Qui |
9 4 3 - · - = - 8 3 2 |
| G + kSept = Ok |
9 16 - · —— = 2 8 9 |
| kT + gT = Qui |
6 5 3 - · - = - 5 4 2 |
| gT + Qua = gSext |
5 4 5 - · - = - 4 3 3 |
| gT + Qui = gSept |
5 3 15 - · - = —— 4 2 8 |
| gT + kSext = Ok |
5 8 - · - = 2 4 5 |
| Qua + Quin = Ok |
4 3 - · - = 2 3 2 |
Die Umkehrung der Addition ist die Subtraktion.
Beispiel: Welches Intervall x muss ich zur Quarte addieren, um die Oktav zu erhalten?
Qua + x = Ok.
Nach Definition nennt man dieses Intervall die Differenz: x = Ok - Qua.
Hier: Ok - Qua = Qui.
Entsprechende Frequenzverhältnisse werden dividiert.
Damit sind auch zum Beispiel folgende Beziehungen verständlich:
| Ok - Qua = Qui |
4 3
2:- = -
3 2
|
| Ok - Qui = Qua |
3 4
2:- = -
2 3
|
| Qui + Qui - Ok = G |
3 3 9 -·-:2 = - 2 2 8 |
Satz: Die Oktave Ok, die Quinte Qui und die große Terz gT sind die Grundintervalle der reinen Stimmung.
Deshalb nennt man dieses System auch das Quint-Terz-System
Das heißt: Alle in Lektion 1 erwähnten Intervalle kann man damit zusammensetzen.
Beweis :
| Die Oktave | Ok Grundintervall |
| Die Quinte | Qui Grundintervall |
| Die Quarte | Qua = Ok - Qui |
| Die große Terz | gT Grundintervall |
| Die kleine Sext | kSext = Ok - gT |
| Die kleine Terz | kT = Qui - gT |
| Die große Sext | gSext = Ok - (Qui -gT) = Ok + gT - Qui |
| Der große Ganzton | G = Qui + Qui - Ok |
| Der kleine Ganzton | G- = gT - G = Ok + gT - Qui - Qui |
| Die kleine Septime | kSept = Ok - G = 2Ok - 2Qui |
| Die kleine Septime | kSept+ = Ok - (G-) = Qui + Qui - gT |
| Der Halbton | H = Qua - gT = Ok - Qui -gT |
| Die große Septime | gSept = Ok - H = Qui + gT |
Mit diesen Intervallen kann man die reine Dur- und Molltonleiter aufbauen.
Reine Tonleiter heißt: Die Dreiklänge der Tonika, Dominante und Subdominante sind aus reinen großen und kleinen Terzen aufgebaut.
Zum Beispiel berechnen sich in der C-Durtonleiter mit dem Grundton c' mit 264 Hz die übrigen Töne mit ihren Frequenzen folgendermaßen:
Beim ersten Lesen können Sie die Eulersche Schreibweise (,e' = Tiefkomma e' usw.) überlesen.
| Ton + Intervall | Berechnung der Frequenz |
| c' + gT = ,e' | 264·5/4 = 330 |
| ,e' + kT = g' | 330·6/5 = 396 |
| g' + gT = ,h' | 396·5/4 = 495 |
| ,h' + kT - Ok = d' | 495·6/5:2 = 297 |
| c' + Ok = c'' | 264·2 = 528 |
| c'' - kT = ,a' | 528:(6/5) = 440 |
| ,a' - gT = f' | 440:(5/4) = 352 |
Zur C-Dur-Tonleiter gehören folglich folgende Frequenzen:
| c' | d' | ,e' | f' | g' | ,a' | ,h' | c'' |
| 264 | 297 | 330 | 352 | 396 | 440 | 495 | 528 |
Beim ersten Lesen können Sie die Eulersche Schreibweise ('es = Hochkomma es usw.) überlesen
Entsprechend kann man die c-Moll-Tonleiter so berechnen, dass die Mollakkorde
c' - 'es' - g', g' - 'b' - d'' und f' - 'as' - c'' aus kleiner Terz und großer Terz aufgebaut sind.Zur C-Moll-Tonleiter (harmonisch absteigend) gehören folglich folgende Frequenzen:
| c' | d' | 'es' | f' | g' | 'as' | 'b' | c'' |
| 264 | 297 | 316,8 | 352 | 396 | 422,4 | 475,2 | 528 |
Modulationen in der reinen Stimmung
Faustregel: Bei einer Modulation in eine Nachbartonart ändern sich zwei Töne, einer davon erkennbar mit Vorzeichenwechsel, der andere geringfügig um ein syntonisches Komma. (Frequenzverhältnis 81/80≡21,5 Cent. Das ist ungefähr 1/5 Halbton.)Zum Beispiel erniedrigt sich bei einer Modulation von C-Dur nach F-Dur nicht nur das H um einen Halbton zu B, sondern auch das D um ein syntonisches Komma. Bei einer Modulation von c-Moll nach f-Moll erniedrigt sich das B um ein syntonisches Komma und das D um einen Halbton zu Des.
Entsprechend erhöht sich bei einer Modulation von C-Dur nach G-Dur nicht nur das F um einen Halbton zu Fis, sondern auch das A um ein syntonisches Komma. Bei einer Modulation von c-Moll nach g-Moll erhöht sich das F um ein syntonisches Komma und das As um einen Halbton zu A.
Das Thema wird in Lektion 7 vertieft.
chromatische Halbton kleiner als der diatonische Halbton. Weiterlesen...
Ein ziemlich mathematische Vertiefung in das Quint-Terz-Sytem der reinen Stimmung finden Sie hier ...
Weiter mit ...
- Lektion 1 Töne, Intervalle, Frequenzen und Frequenzverhältnisse
- Lektion 2 Hintereinanderausführung zweier Tonschritte. Reine Stimmung
- Lektion 3 Beschreibung von Tonsystemen ohne Akustik
- Lektion 4 Das Centmaß für Intervalle
- Lektion 5 Die gleichstufige Stimmung
- Lektion 6 Das pythagoreische und syntonische Komma
- Lektion 7 Eulersches Tonnetz - Modulationen
- Lektion 8 Mitteltönige und wohltemperierte Stimmungen
- Lektion 9 Der Akkord der 2. Stufe, die Kommafalle, der neapolitanische Sextakkord und die Doppeldominante
