Die Homepage von Joachim Mohr
FAQWann schneiden sich drei Geraden in einem Punkt?
Antwort: Die drei Geraden seien durch die folgenden Gleichungen gegeben:a1x + b1y + c1 = 0
a2x + b2y + c2 = 0
a3x + b3y + c3 = 0
Dann schneiden sich die Geraden in einem Punkt, wenn gilt:
die drei Vektoren (a1,b1,c1),(a2,b2,c2) und (a3,b3,c3) sind linear abhängig.
Das ist genau dann der Fall, wenn die folgende Determinante Null ist:
|a b c | | 1 1 1| |a b c | = a b c + b c a + c a b - c b a - a c b - b a c = 0 | 2 2 2| 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 |a b c | | 3 3 3|
Beispiel:
1 7 1 7 3
y = -x + - y= - ——x + - y = -x - 2
9 9 12 6 2
Auf die Form
Ergebnis: Die Geraden schneiden sich in einem Punkt.
Schneller ist jedoch die direkte Berechnung: Der Schnittpunkt der beiden ersten Geraden errechnet sich zu S(2|1). Eingesetzt in die dritte Gleichung zeigt sich: S liegt auch auf der dritten Geraden. | 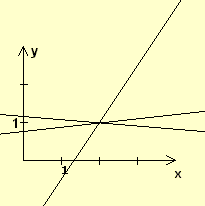
|
Wann liegen drei Punkte auf einer Geraden?
Antwort: Die Drei Punkte A1(x1|y1), B2(x2|y2) und C3(x3|y3) liegen auf einer Geraden,wenn die folgende Determinante Null ist:
|x y 1| | 1 1 | |x y 1| = x y + y x + x y - y x - x y - y x = 0 | 2 2 | 1 2 1 3 2 3 2 3 1 3 1 2 |x y 1| | 3 3 |Die Determinante ist gleich dem Doppelten des (orientierten) Flächeninhalts des Dreiecks ABC.
Wie berechnet man den Umkreismittelpunkt eines Dreiecks?
Antwort: Das Dreieck habe die Koordinaten A(x1|y1)B(x2|y2)C(x3|y3).Dann berechnet sich der Umkreismittelpunkt U(x|y) zu
1 u 1 v
x = -·- und y = -·-, wobei
2 d 2 d
2 2 2 2 2 2
u = (y -y )·(x + y )+(y -y )·(x + y )+(y -y )·(x + y ),
2 3 1 1 3 1 2 2 1 2 3 3
2 2 2 2 2 2
v = (x -x )·(x + y )+(x -x )·(x + y )+(x -x )·(x + y ) und
3 2 1 1 1 3 2 2 2 1 3 3
d = x y + x y + x y - x y - x y - x y .
1 2 2 3 3 1 1 3 2 1 3 2
———————————————————
/ 2 2
Der Radius ist dann r := \/(x - x ) + (y - y ) .
1 1
Herleitung:
Um den Umkreismittelpunkt zu bestimmen, musst Du den Schnittpunkt zweier Mittelsenkrechten berechnen.Den Rechenvorgang kann man dem folgenden Computer-Algebra-Programm (Maple) entnehmen:
> restart; #x1:=1;y1:=1;x2:=8; y2:=1; x3:=3;y3:=7;#Koordinaten von A1, B2 und C3
> u1:=(x1+x2)/2; v1:=(y1+y2)/2; m1z:=x1-x2; m1n:=y2-y1;#Mittelsenkrechte von AB mit Steigung m1z/m1n
u2:=(x1+x3)/2; v2:=(y1+y3)/2; m2z:=x1-x3;m2n:=y3-y1; #Mittelsenkrechte von AC mit Steigung m2z/m2n
> #Die Gerade durch M1(u1|v1) mit der Steigung m1z/m1n hat die Gleichung
#y-v1=m1z/m1n*(x-u1) bzw.m1n*(y-v1)=m1z*(x-u1) (1)
#Die Gerade durch M2(u1|v2) mit der Steigung m2z/m2n hat die Gleichung
#m2n*(y-v2)=m2z*(x-u2) (2). Die Lösung des LSG (1) und (2) ergibt den Schnittpunkt:
solve({m1n*(y-v1)=m1z*(x-u1) , m2n*(y-v2)=m2z*(x-u2)},{x,y});
Die allgemeine Lösung lautet (aus Maple kopiert):
x = 1/2*(y3*y2^2-y3*y1^2+y1*y3^2-y3*x1^2+y1*x3^2+y3*x2^2-y1*y2^2
-y1*x2^2+y2*x1^2-y2*y3^2+y2*y1^2-y2*x3^2)/D
y = 1/2*(-y1^2*x2+y1^2*x3+y3^2*x2-x1^2*x2+x1*y2^2-x1*x3^2+x3^2*x2
+x1^2*x3+x1*x2^2-x3*x2^2-x3*y2^2-x1*y3^2)/D
(x und y in eine Zeile schreiben), wobei
der Nenner D gleich der Determinante der folgenden Matrix ist:
| x1 y1 1 |
| |
D= | x2 y2 1 | = x1y2 + x2y3 + x3y1 - x1y3 - x2y1 - x3y2.
| |
| x3 y3 1 |
D ist gleich dem Doppelten des Flächeninhalts des Dreiecks ABC,
wird also nie Null, wenn nicht A, B und C auf einer Geraden liegen.
Der Radius des Umkreises ist dann der Abstand von U zu A, B oder C.
Rechenschema:
x1= y1= x2= (Hier die Koordinaten von A, B und C einsetzten) y2= x3= y3= D=x1*y2+x2*y3+x3*y1-x1*y3-x2*y1-x3*y2 x0=1/2*(y3*y2^2-y3*y1^2+y1*y3^2-y3*x1^2+y1*x3^2+y3*x2^2-y1*y2^2-y1*x2^2+y2*x1^2-y2*y3^2+y2*y1^2-y2*x3^2)/D y0=1/2*(-y1^2*x2+y1^2*x3+y3^2*x2-x1^2*x2+x1*y2^2-x1*x3^2+x3^2*x2+x1^2*x3+x1*x2^2-x3*x2^2-x3*y2^2-x1*y3^2)/D r=sqrt((x1-x0)^2+(y1-y0)^2) Probe r=sqrt((x2-x0)^2+(y2-y0)^2) r=sqrt((x3-x0)^2+(y3-y0)^2)Beispiel (mit Rechenblatt aus TTMathe berechnet): 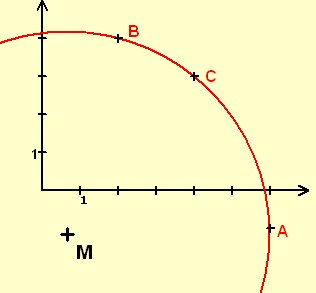
x1=6 y1=-1 x2=2 y2=4 x3=4 y3=3 D=...=-6 x0=...=2/3 y0=...=-1 1/6=-1,166666667 r=sqrt((x1-x0)^2+(y1-y0)^2)=5/6*sqrt(41)=5,335936865 Probe r=sqrt((x2-x0)^2+(y2-y0)^2) =5/6*sqrt(41)=5,335936865 r=sqrt((x3-x0)^2+(y3-y0)^2) =5/6*sqrt(41)=5,335936865 |
Wie gibt man einen Kreisbogen durch drei Punkte an?
Antwort: Die drei Punkte seinen A(x1|y1)B(x2|y2)C(x3|y3).Als erstes berechnet man den Umkreismittelpunkt U(x0|y0) und den Radius r des Umkreises der drei Punkte.
Als zweites sei bemerkt, wie man einen Kreisbogen darstellen kann:
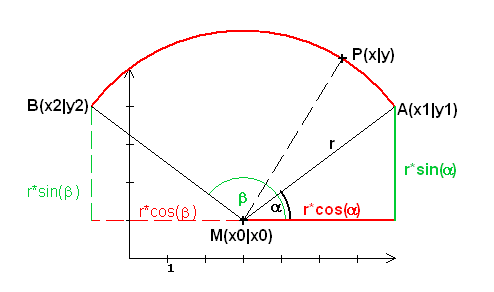 |
Die Koordinaten der Punkte P(x|y) auf dem Kreisbogen kann man in der "Parameterdarstellung"
folgendermaßen angeben:
x=x0 + r·cos(φ) y=y0 + r·sin(φ)wobei der Winkel φ das Intervall von α bis β durchläuft. |
Als drittes fehlt noch: Wie kann ich die Winkel α aus A und M berechnen (und entsprechend den Winkel β)?
Dazu muss ich die Gleichung
y1 - y0
tan(α) = ——————— nach α auflösen:
x1 - x0
|
Eine Schwierigkeit besteht darin, dass die Funktionen tan nicht
umkehrbar ist.
Die Umkehrfunktion arctan von tan liefert nur Werte von -90° bis +90°.
y
Ist zum Beispiel tanα = - für α aus dem Intervall [0;360°] und
x
y
α1 = arctan(-), dann gilt:
x
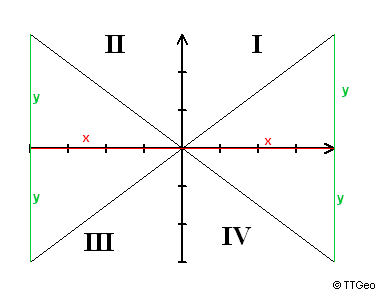
α = α1, falls x > 0 und y > 0, (α im I. Quadranten)α = α1 + 180° falls x < 0 und y > 0 (α im II. Quadranten), α = α1 + 180° falls x < 0 und y < 0 (α im III. Quadranten) oder α = α1 + 360° falls x > 0 und y < 0 (α im IV. Quadranten). |
Beispiel:

|
Berechnung des Winkels α,
der Winkel M(3|1)A(7|4) zur Horizontalen
yd=y1-y0=3
xd=x1-x0=4
xd>0 yd>0 also
α=arctan(yd/xd)=36,87°
Berechnung des Winkels β,
der Winkel M(3|1)B(-1|4) zur Horizontalen
yd=y2-y0=3
xd=x2-x0=-4
xd>0 yd>0 also
β=arcta(yd/xd)+180°=143,13°
Der Kreisbogen von A nach B mit Mittelpunkt M hat
dann die Parameterdarstellung:
x= 3 + 5cos(φ)
(36,87° ≤ φ ≤ 143,13°)
y= 1 + 5sin(φ)
|
a1=3 + 5*cos(α + dφ/n) b1=1 + 5*sin(α + dφ/n) a2=3 + 5*cos(α + 2*dφ/n) b2=1 + 5*sin(α + 2*dφ/n) a3=3 + 5*cos(α + 3*dφ/n) b3=1 + 5*sin(α + 3*dφ/n) ...Hinweis: Der "Komplememntär-"Kreisbogen von A nach B (der Bogen, der zum Vollkreis noch fehlt)hat die Parameterdarstellung:
x= 3 + 5cos(φ)
(143,13° ≤ φ ≤ 396,87°=36,87°+360°)
y= 1 + 5sin(φ)
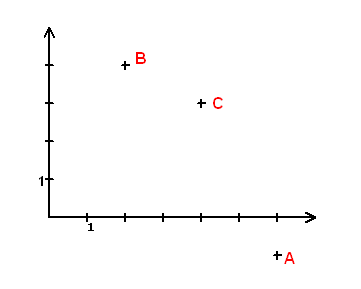 |
Aufgabe: Der Kreisbogen von A(6|-1) nach C(4|3) über B(2|4) soll in 10 gleiche Abschnitte geteilt werden.
Versuche, bevor Du die Lösung anschaust, Dir zunächst vorzustellen, wie die Lösung
ausschauen könnte.
Die folgende Rechnung zeigt das Rechenschema für das Rechenblatt von TTMathe. Bei anderen Werten müssen nur die Anfangszeilen entsprechend geändert werden.
(Die gesamte Rechnung wird im Bogenmaß durchgeführt. Zur Veranschaulichung habe ich die Winkel noch ins Gradmaß
umgerechnet.)
|
x1=6 y1=-1 x2=2 y2=4 x3=4 y3=3 D=x1*y2+x2*y3+x3*y1-x1*y3-x2*y1-x3*y2 x0=1/2*(y3*y2^2-y3*y1^2+y1*y3^2-y3*x1^2+y1*x3^2+y3*x2^2-y1*y2^2-y1*x2^2+y2*x1^2-y2*y3^2+y2*y1^2-y2*x3^2)/D y0=1/2*(-y1^2*x2+y1^2*x3+y3^2*x2-x1^2*x2+x1*y2^2-x1*x3^2+x3^2*x2+x1^2*x3+x1*x2^2-x3*x2^2-x3*y2^2-x1*y3^2)/D r=sqrt((x1-x0)^2+(y1-y0)^2) Probe r=sqrt((x2-x0)^2+(y2-y0)^2) r=sqrt((x3-x0)^2+(y3-y0)^2)Ergebnis: Mittelunkt M(x0|y0) = M(2/3|1 1/6) Rdius r=5/6*sqrt(41).
Als nächstes rechnen wir die Winkel von MA, MB, MC zur Horinzontalen aus:
Berechnung des Winkels MA zur Horizontalen
yd=y1-y0
xd=x1-x0
xd>0 yd>0 also
wa=arctan(yd/xd)
Berechnung des Winkels MB zur Horizontalen
yd=y2-y0
xd=x2-x0
xd>0 yd>0 also
wb=arctan(yd/xd)
Berechnung des Winkels MC zur Horizontalen
yd=y3-y0
xd=x3-x0
xd>0 yd>0 also
wc=arctan(yd/xd)
Ergebnis: Winkel MA zur Horizontalen: wa=0,031239833=1,8°
Winkel MB zur Horizontalen: wb=1,318242051=75,5°
Winkel MC zur Horizontalen: wc=0,896055385=51,3°
Der Kreisbogen von A nach C über B verläuft mathematisch negativ.
Der mathematisch positive Verlauf geht dann von C nach A mit den zugehörigen Winkeln:
wc=51,3° und wa'=361,8° (=qa+360°).
Parameterdarstellung des Kreisbogens von C nach A (über B).
x=x0 + r*cos(φ)
wc ≤ φ ≤ wa'
y=y0 + r*sin(φ)
Die Koordinaten der Zwischenpunkte P1(a1|b1), P2(a2|b2) berechnen sich folgendermaßen:
Die Winkeldifferenz wa' - wc (in TTMathe ist 360° erlaubt, in Maple dafür 2*Pi wd=wa+360° - wc Probe: P0=C P10=D a0=x0+r*cos(wc+0*wd/10) =4 b0=y0+r*sin(wc+0*wd/10) =3 a1=x0+r*cos(wc+wd/10) =1,37374796 b1=y0+r*sin(wc+wd/10)=4,122213958 a2=x0+r*cos(wc+2*wd/10) =-1,455064799 b2=y0+r*sin(wc+2*wd/10) =3,729298796 a3=x0+r*cos(wc+3*wd/10) =-3,676055721 b3=y0+r*sin(wc+3*wd/10) =1,933814664 a4=x0+r*cos(wc+4*wd/10) =-4,652967675 b4=y0+r*sin(wc+4*wd/10) =-0,749878124 a5=x0+r*cos(wc+5*wd/10) =-4,105940354 b5=y0+r*sin(wc+5*wd/10) =-3,552970177 a6=x0+r*cos(wc+6*wd/10) =-2,191683105 b6=y0+r*sin(wc+6*wd/10) =-5,672447266 a7=x0+r*cos(wc+7*wd/10) =0,541418298 b7=y0+r*sin(wc+7*wd/10) =-6,501133376 a8=x0+r*cos(wc+8*wd/10) =3,310400158 b8=y0+r*sin(wc+8*wd/10) =-5,801631117 a9=x0+r*cos(wc+9*wd/10) =5,322019943 b9=y0+r*sin(wc+9*wd/10) =-3,774330007 a10=x0+r*cos(wc+10*wd/10) =6 b10=y0+r*sin(wc+10*wd/10)=-1
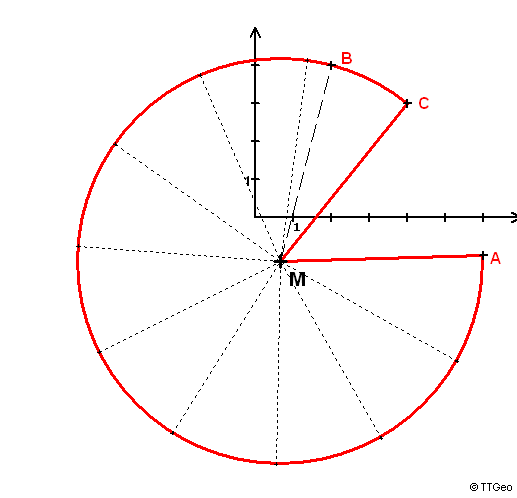
Ergebnis: Die Teilpunkte sind:
P0(4|3) = C P1( 1,373747960| 4,122213958) P2(-1,455064799| 3,729298796) P3(-3,676055721| 1,933814664) P4(-4,652967675|-0,749878124) P5(-4,105940354|-3,552970177) P6(-2,191683105|-5,672447266) P7( 0,541418298|-6,501133376) P8( 3,310400158|-5,801631117) P9( 5,322019943|-3,774330007) P10(6|-1) = A |
 |
Wie berechnet man die Ausgleichsgerade durch viele Punkte (Lineare Regression)
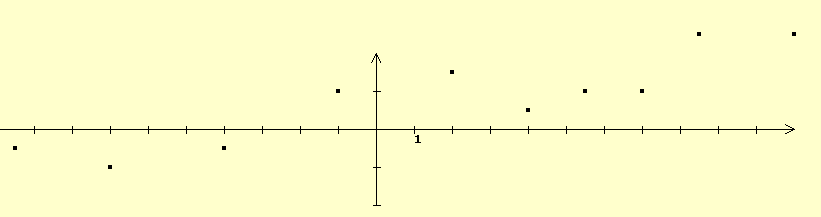
Man weiß theoretisch, dass ein gesuchter Zusammenhang eine lineare Funktion ist. Wenn man die Messwerte in ein Koordinatensystem einträgt, sollten alle Punkte auf einer Geraden liegen. Nun sind die Messwerte mit Ungenauigkeiten behaftet. Deswegen begnügt man sich auch nicht mit zwei Werten sondern mit möglichst vielen und sucht dann eine Gerade, die sich den Punkten möglichst gut anpasst.
Gesucht ist also zum Beispiel die Gerade, die sich den Punkte
P1(-9,5|-0,5), P2(-7|-1), P3(-4|-0,5), P4(-1|1), P5(2|1,5), P6(4|0,5), P7(5,5|1), P8(7|1), P9(8,5|2,5) und P10(11|2,5) möglichst gut anpasst.
In unserem Beispiel wäre es die Gerade mit der Gleichung
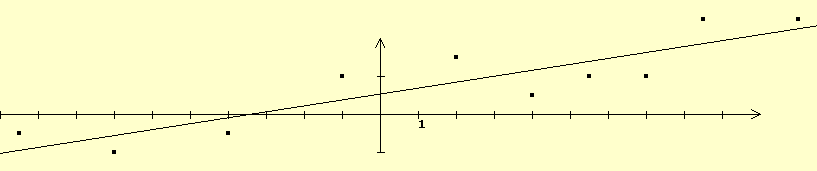
Im allgemeinen Fall hat man die Punkte P1(x1|y1), P2(x2|y2), P3(x3|y3) ... Pn(xn|yn).
Nach Carl Friedrich Gauß bestimmt man die Gerade mit der Gleichung y=m·x + c so, dass die Summe der Fehlerquadrate
S=(m·x1 + c - y1)2 + (m·x2 + c - y2)2 + (m·x3 + c - y3)2 + ... + (m·xn + c - yn)2.
minimal wird.
Mit folgenden Formeln kann man die Steigung m und den y-Abschnitt c berechnen:
Mittelwerte x0=(Summe xi)/n, y0=(Summe yi)/n
Fehlerquadratsumme Sxx=Summe(xi-x0)2, Syy=Summe(yi-y0)2
Fehlerproduktsumme Sxy=Summe(xi-x0)(yi-y0)
Steigung der Geraden m=Sxy/Sxx, y-Abschnitt c=y0-b·x0.
Mittelwerte x0=(Summe xi)/n, y0=(Summe yi)/n
Fehlerquadratsumme Sxx=Summe(xi-x0)2, Syy=Summe(yi-y0)2
Fehlerproduktsumme Sxy=Summe(xi-x0)(yi-y0)
Steigung der Geraden m=Sxy/Sxx, y-Abschnitt c=y0-b·x0.
|
Mit TTMathe kann man die Ausgleichsgerade mit Menü "Algebra|Ausgleichsgerade" berechnen.
Dort gibt man die Werte folgendermaßen ein:
Man kann dort auch die Ausgleichsfunktion y=exp(a*x+b) berechnen. |
Beispiel:
-9 -2,5 -7 -2 -5 -1,5 -3,5 -0,5 -1,5 0 0,5 0,5 3 0 4 1 5 0 6 0,5 7 2 8 2,5 10 1,5 11 2,5 |
Falls bei Ihren Werten ein Strichpunkt zwischen den x- und y-Werten ist, können Sie
diesen vor dem Hineinkopieren in das Eingabefeld von TTMathe durch eine Leerstelle in jedem Textprogramm ersetzten.
TTMathe berechnet dann die Ausgleichsgerade zu: |
In TTGeo wird die Ausgleichsgerade mit Menü
Weiter mit: Affine Räume, Affinitäten, ....
