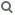Die Homepage von Joachim Mohr
Siehe auch
Affine
Ebenen
Der affine Raum und affine Abbildungen
Diese Datei kann auch als PDF-Datei heruntergeladen werden. Download ...
Der affine Raum
Diese knappe Einführung zu dem Begriff des affinen Raumes soll die Schreibweise
bei den Beispielen von Kongruenzen, Ähnlichkeitsabbildungen, Affinitäten
und Koordinatentransformationen erläutern.
Dem nicht so vertrauten Leser empfehle ich, sich zuerst mit Affinitäten (das sind Verschiebungen, Spiegelungen, Scherungen etc.) oder gleich mit konkreten Beispielen zu beschäftigen und erst bei Bedarf diese abstrakte Einleitung durchzuarbeiten.
Dem nicht so vertrauten Leser empfehle ich, sich zuerst mit Affinitäten (das sind Verschiebungen, Spiegelungen, Scherungen etc.) oder gleich mit konkreten Beispielen zu beschäftigen und erst bei Bedarf diese abstrakte Einleitung durchzuarbeiten.
Definition: Ein affiner Raum wird durch ein Tripel (PR,VR,Pfeil) beschrieben:
PR heißt Punktraum, seine Elemente Punkte,
VR ist ein Vektorraum, seine Elemente werden als Vektoren bezeichnet, und
Pfeil: (A,B) -› Pfeil(A,B) ist eine Abbildung von PR×PR in VR (PR×PR: das kartesische Produkt von PR und PR). Das heißt: Jedem Punktpaar A,B ist ein eindeutig bestimmter Vektor zugeordnet.
Künftig verwenden wir die Schreibweise:
——› AB = Pfeil(A,B)Neben den Vektorraumaxiomen gelten noch folgende zwei Axiome, die Punktraum und Vektorraum verbinden.
-›
I Zu jedem Punkt A und jedem Vektor v gibt es einen
-› ——›
eindeutig bestimmten Punkt B mit v = AB.
-›
Bezeichnung: B = A + v.
Eindeutig heißt:
-› ——› ——›
Wenn v = AB und v = AB , so folgt daraus: B = B .
1 2 1 2
-› ——› -›
Es gilt deshalb stets: v = AB ‹=› B = A + v .
Dieses "+" ist nicht die Addition von Vektoren, sondern ist eine Verknüpfung
von einem Punkt und einem Vektor und eben durch Axiom I definiert:
"Das Ansetzen von Vektor v an Punkt A ergibt B".
——› ——› ——›
II Für alle Punkte A,B,C gilt: AB + BC = AC.
Folgerungen:
——› -›
a) Beh.: Für alle Punkte A gilt: AA = o
(Nullvektor)
——› ——› ——›
Beweis: AA + AA = AA (nach II).
——›
Ziehen wir auf beiden Seiten den Vektor AA ab,
——›
so erhalten wir AA = 0 ∎
——› ——›
b) Beh.: Für alle Punkte A und B gilt: BA = - AB
——› ——› ——› -› ——› ——›
Bew.: AB + BA = AA = o => BA = - AB ∎
c) Beh.:
-› -›
Für alle Punkte A und alle Vektoren v , w gilt:
-› -› -› -›
A + (v + w ) = (A + v ) + w
-› -›
Beweis: Sei A + v = B und B + w = C.
-› ——› -› ——›
Beweis: Dann folgt: v = AB und w = BC
-› -› ——› ——› ——›
und daraus v + w = AB + BC = AC .
-› -› -›
Somit (A + v ) + w = B + w = C
-› -›
und A + (v + w ) = C. ∎
——› ——› ——› ——›
d) Beh.: AB = DC ‹=› AD = BC
(Paralleogrammregel: Ein Viereck, bei denen zwei Gegenseiten gleich lang und parallel sind, ist ein Parallelogramm)
——› ——› ——› ——› ——› ——› ——› ——› ——›
Bew.: AB = DC => AD = AB + BC + CD = AB + BC - DC
——› ——› ——› ——›
= AB + BC - AB = BC
Die andere Richtung "‹=" wird genauso bewiesen. ∎
Koordinaten eines Punktes
Jedem Punkt P eines affinen Raumes kann man Koordinaten bezüglich eines Koordinatensystems zuordnen.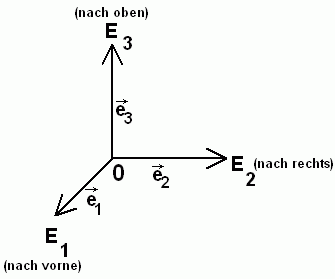
Zunächst wählt man einen beliebigen Punkt O als Ursprung.
Ist der zugeordnete Vektorraum zum Beispiel dreidimensional, dann wählt man noch eine Basis des zugeordneten Vektorraumes, etwa
-› -› -› (e ,e ,e ) 1 2 3Hinweis die Punkte O, E1, E2 und E3 mit
-› -› -›
E = O + e , E = O + e und E = O + e
1 1 2 2 3 3
nennt man "Punkte in allgemeiner Lage".
Jeder Punkt P hat dann eindeutig die Darstellung
-› -› -›
P = O + x ·e + x ·e + x ·e
1 2 2 3 3
-› -› -›
und wird - wenn das Koordinatensystem (O, e ,e ,e ) klar ist
1 2 3
mit P(x |x |x ) bezeichnet.
1 2 3
Durch diese Zuordnung erhält man eine Affinität f
(siehe unten) des affinen Raumes in R3.
|x1|
| |
Der Bildpunkt von P ist dann f(P) = |x2|
| |
|x3|
-› ——›
(Der "Ortsvektor" x = OP von P).
-› -› -›
Hat man ein zweites Koordinatensystem K2= (O', e' ,e' ,e')
1 2 3
mit der zugeordneten Affinität
|x1'|
| |
P -› g(P) = |x2'|, wobei dann P bezüglich
| |
|x3'|
des zweiten Koordinatensystem folgende Koordinaten hat:
P (x', x' ,x'),
bez. K2 1 2 3
|x1'| |x1|
| | -1 | |
so kann man die Koordinaten |x2'| = g(f (|x2|)
| | | |
|x3'| |x3|
über eine Koordinatentransformation
|x1'| |x1| |a d g| |x1| |j|
| | -1 | | | | | | | |
|x2'| = g(f (|x2|) = |b e h|·|x2| + |k|
| | | | | | | | | |
|x3'| |x3| |c f i| |x3| |l|
|x1|
| |
aus den Koordinaten |x2| berechnen.
| |
|x3|
 Beispiel.
Beispiel.
Beispiel R3
Siehe: Lektionen der Vektorrechnung.
Die Punkte des R3 sind zum
Beispiel A(4|5|4) und B(6|8|9).
Dann ist der ("Verbindungs-")Vektor
-› ——› 2
v = AB = (3). Setzt man umgekehrt
5
den Vektor v an A an, so erhält man
den Punkt B:
-› 2
A + v = A(4|5|4) + (3) = B(6|8|9).
5
Bei vielen Betrachtungen wird auf Punkte
verzichtet, sondern nur mit Vektoren gerechnet:
Statt der Punkte A, B , ...
verwendet man "Ortsvektoren" (hellgrün)
-› ——› 4 -› ——› 5
a = OA = (3), b = OB (5), ...,
2 5
Im Grunde sind dann die Punkte des affinen Raumes die Vektoren und der zugehörige
Vektorraum die Translationen (Parallelverschiebungen).
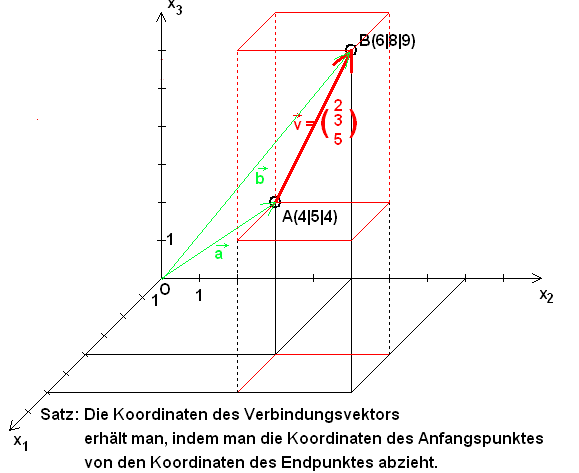
-› -› -› 6 4 2
v = b - a = (8) - (5) = (3)
9 4 5
In jedem Lehrgang zur Vektorrechnung und
affinen Räumen erarbeitet man mit Hilfe einer Basis des Vektorraumes
und Einführung eines Ursprungs im Affinen Raum folgenden ...
Satz: Jeder Vektorraum der Dimension n ist isomorph zu Kn,
wobei K der zugeordnete (Schief-)Körper ist.
Jeder affine Raum der Dimension n ist isomorph zu Kn.
(n endlich oder - als Kardinalzahl - unendlich.)
Satz: Jeder Vektorraum der Dimension n ist isomorph zu Kn,
wobei K der zugeordnete (Schief-)Körper ist.
Jeder affine Raum der Dimension n ist isomorph zu Kn.
(n endlich oder - als Kardinalzahl - unendlich.)
Affine Abbildungen, Ähnlichkeitsabbildungen, Kongruenzen
Im folgenden seinen die affinen Räume mindestens 2-dimensional.Die Geraden des affinen Raumes sind die Punktmengen der Form
-›
g = {A + x·v | x ε K} für die Punkte A und von 0
-›
verschiedenen Vektoren v , d.h.
für alle Punktepaare (A,B) auf g gilt:
——› -›
AB ist linear abhängig von v .
Drei verschiedene Punkte A,B,C heißen kollinear, wenn
wenn sie auf einer Geraden liegen.
Definition:
I Eine bijektive Abbildung eines Punktraumes auf einen Punktraum heißt Affinität, wenn die Bildpunkte dreier kollinearer Punkte wieder kollinear und umgekehrt die Urbildpunkte dreier kollinearer Punkte kollinear sind.
Ist α eine Affinität, so werden Geraden g wieder auf Geraden g'=α(g) abbgebildet und das Urbild g=α-1(g') einer Geraden ist wieder eine Gerade.
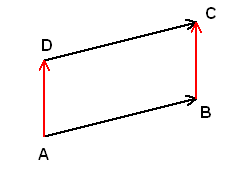
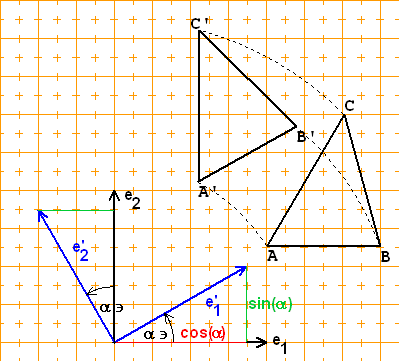
Beh.: Eine Affinität α bildet ein Parallelogramm ABCD auf ein Parallelogramm A'B'C'D' ab.
Beweis: Sei M der Schnittpunkt der Diagonalen des Parallelogramms ABCD. Dann ist M' der Schnittpunkt des Vierecks A'B'C'D. Folglich liegt das Viereck A'B'C'D' in einer Ebene (2-dim. affiner Unterraum).
Die Geraden (A'B') und (D'C') schneiden sich nicht (sonst hätten auch AB und DC einen Schnittpunkt). Sie sind also weder winschief noch haben sie einen Schnittpunkt. Also sind sie parallel. Analog folgt, dass die Geraden (B'C') und (A'D') parallel sind. ∎
Anhand dieser Figur sieht man auch, dass die Mitte M von BD auf die Mitte M' von B'C' abgebildet wird. Eine Folgerung daraus ist: Eine Affinität ist teilverhältnistreu. (Jedenfalls für alle rationalen Teilverhältnisse. Für "irrationale" Teilverhälnisse muss noch die Stetigkeit algebraischer Operationen in K vorausgesetzt werden. Für reelle oder komplexe Skalare ist diese Voraussetzung erfüllt. Im Folgenden setzten wir die Teilverhältnistreue voraus.)
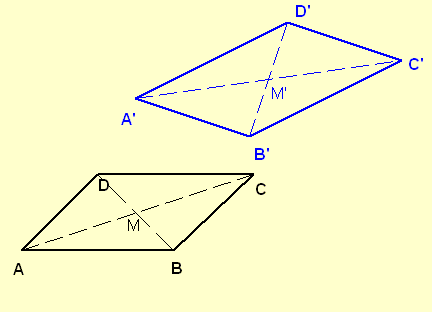
Eine Affinität α induziert somit durch folgende wohldefinierte Definition eine bijektive lineare Abbildung α des zugehörigen Vektorraumes
-› ———› ——›
α(v ) = A'B' für v = AB.
α ist lineare Abbildung, da gilt:
-› -› ————› ———› ———› -› -› ——› ——›
α(v + w) = A'C' = A'B' + B'C' = α(v ) + α(w ) für v=AB und w=BC
-› -› -›
und α(k·v ) = k·v für alle Skalare k und Vektoren v ,
da α teilverhältnistreu ist.
Im Sinne der Informatik haben wir es bei einer Affinität α mit "überladenen" Funktionen zu tun.
α: A -› A' (Punkt auf Punkt)
αG: g -› g' (Gerade auf Gerade)
-› -›
αV: v -› v' (Vektor auf Vektor)
Zwischen den verschiedenen Abbildung α, αG und αV kann es keine Verwechsung
geben, deshalb kann man sie (und wurden sie hier) mit dem gleichen Symbol bezeichnen: α=αG=αV.
Hinweis: In der Literatur trifft man auf den Begriff der "affinen Abbildung". Dabei
wird die Bijektivität nicht gefordert.
Ist der affine Raum euklidisch, das heißt existiert auf P noch eine Metrik, (A,B) -› d(A,B) ε R, so kann man noch definieren:
II Eine Affinität f heißt Ähnlichkeitsabbildung, wenn ein Faktor k ‹› 0 so existiert,
dass d(f(A),f(B)) = k·d(A,B) für alle A,B ε P. (k heißt Streckfaktor.)
III Eine Affinität f heißt Kongruenzabbildung, wenn d(f(A),f(B)) = d(A,B) für alle A,B El. P.
Mit der Metrik auf P ist ein Skalarprodukt des Vektorraum
verbunden, auf das ich hier nicht eingehen brauche. Wichtig
dabei ist nur der Begriff "orthogonal".
-› -› -›
Hat man ein Koordinatensystem (O,e ,e ,...,e ) des affininen Raumes,
1 2 n
-› -› -›
so ist (O', e', e', ... , e') ebenfalls ein Koordinatensystem.
1 2 n
Ist das Koordinatensystem ein kartesisches,
-› -› -›
die Basis (e ,e ,..., e ) also eine Orthonormalbasis des Vektorraumes,
1 2 n
so ist die zugehörige Affinität ähnlich,
-› -› -›
wenn die Vektoren e',e',..., e' paarweise
1 2 n
orthogonal und gleich lang sind.
Die Ähnlichkeit ist dann eine Kongruenz(-abbildung), wenn
(e', e', ... , e') ebenfalls eine Orthonormalbasis ist.
1 2 n
Affinitäten im R2
I Allgemein
Die Abbildungsgleichungen beziehen sich auf das
-› -›
Standardkoordinatensystem (O, e , e )
1 2
-› 1 0
mit O=O(0|0) und e = ( ), und e = ( ).
1 0 2 1
Das Koordinatensystem ist festgelegt durch die
Punkte O(0|0), E (1|0), E (0|1).
1 2
Eine Affinität wird dann dargestellt
durch die Abbildungsgleichungen:
-› a c -› e
x' = ( )x + ( ) oder
b d f
-› -› -› a c -› e
x' = A·x + b mit A =( ) und b = ( ).
b d f
a c
Die Multiplikation der Matrix M = ( )
b d
-› x1
mit einem Vektor x = ( ) ist definert als
x2
-› a c x1 a·x1 + c·x2
M·x = ( )·( ) = ( )
b d x2 b·x1 + c·x2

Für P(x |x ) und P'(x'|x') mit
1 2 1 2
-› x ——› x'
x = ( ) und x' = ( )
x x'
2 2
——› e
sowie OO' = ( ) gilt:
f
-› ——› ———› a c
x' = OP' = OO' + ( )·x + ( )·x
b 1 d 2
a c e
= ( )·x + ( )·x2 + ( )
b 1 d f
a c -› e
=( )x + ( )
b d f
-› a -› -› c
O wird auf O'(e|f), e auf e' = ( ) und e auf e' = ( ) abgebildet.
1 1 b 2 2 d
Die Affinität ist eine Ähnlichkeitsabbildung, wenn
a c
die Vektoren ( ) und ( ) senkrecht aufeinander stehen
b d
und gleich lang sind, d.h
2 2 2 2
wenn ac + bc = 0 und a + b = c + d ist.
Die Affinität ist eine Kongruenzabbildung, wenn
a c
die Vektoren ( ) und ( ) senkrecht aufeinander stehen
b d
und die Länge 1 haben, d.h
2 2 2 2
wenn ac + bc = 0, a + b = 1 und c + d = 1 ist.
c
Diese Eigenschaft ist unabhängig vom "Verschiebungsvektor" ( ).
d
Um die Abbildungsmatrix aufzustellen, genügt es deshalb,
-› a -› 1
das Bild e' = ( ) von e = ( )
1 b 1 0
-› c -› 0
und das Bild e' = ( ) von e = ( ) zu finden.
2 d 2 1
Die Abbildungsgleichung der Verkettung von Abbildungen berechnet sich folgendermaßen:
——› a1 c1 -› e1
Sei die erste Abbildung x' = ( )·x + ( ) ,
b1 d1 f1
——› a2 c2 -› e2
und die zweite Abbildung x'' = ( )·x' + ( )
b2 d2 f2
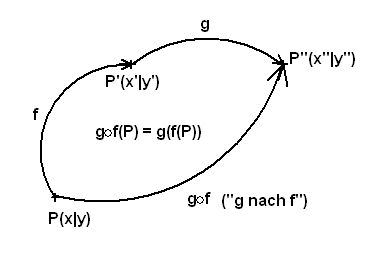
Dann gilt für die Verkettung (=Hintereinanderausführung)
der beiden Abbildungen:
——› a2 c2 a1 c1 -› e1 e2
x'' = ( )·[( )·x + ( )] + ( ) , also
b2 d2 b1 d1 f1 f2
——› a3 c3 -› e3 a3 c3 a1 c1 a2 c2
x'' = ( )·x + ( ) mit ( ) = ( )·( )
b3 d3 f3 b3 d3 b1 d1 b2 d2
e3 a2 c2 e1 e2
und ( ) = ( )·( ) + ( ).
f3 b2 d2 f1 f2
Das Produkt der zwei Matrizen oder einer Matrix mit einem Vektor ist hier:
a1 c1 a2 c2 a1a2+c1b2 a1c2+c1d2
( )·( ) = ( )
b1 d1 b2 d2 b1a2+d1b2 b1c2+d1d2
a2 c2 e1 a2e1+c2f1
und ( )·( ) = ( ).
b2 d2 f1 b2e1+d2f1
Die Umkehrabbildung der Affinität
-› a c -› e
x' = ( )·x + ( ) wird ermittelt,
b d f
-›
indem diese Gleichung nach x aufgelöst wird:
a c -› ——› e -› a' c' -› a' c' e
( )·x = x' - ( ) => x = ( )x' - ( )·( ) wobei
b d f b' d' b' d' f
a' c' 1 d -c a c
( ) = ———————·( ) die inverse Matrix von ( ) ist.
b' d' ad - bc -b a b d
Da Affinitäten stets umkehrbar sind,
ist die Determinante D = ad - bc ≠ 0.
-› -›
Nach Vertauschen von x' und x erhält man als
Abbildungsgleichung der Umkehrabbildung:
———————————————————————————————
| -› a' c' -› a' c' e |
| x' = ( )x - ( )·( ) |
| b' d' b' d' f |
———————————————————————————————
Die Umkehrabbildungen der folgenden Abbildungen (siehe unten) sind:
-› -1 0 -›
I a) Punktspiegelung: x' = ( )x
0 -1
-› -1 0 -›
Umkehrabbildung: x' = ( )x (dieselbe)
0 -1
-› -1 0 -› 6
b) Punktspiegelung: x' = ( )x + ( )
0 -1 4
-› -1 0 -› 6
Umkehrabbildung x' = ( )x + ( ) (dieselbe)
0 -1 4
——› cos(a) - sin(a) -› -›
c) Drehung: x' = ( )x )x
sin(a) + cos(a)
——› cos(a) + sin(a)
Umkehrabbildung: x' = ( )
-sin(a) + cos(a)
d) Drehung um Z(e|f): Drehung:
-› cos(a) - sin(a) -› cos(a) + sin(a) e
x' = ( )x - ( )·( )
sin(a) + cos(a) -sin(a) + cos(a) f
Umkehrabbildung:
cos(a) + sin(a) -› cos(a) + sin(a) e
x' = ( )x - ( )·( )
-sin(a) + cos(a) -sin(a) + cos(a) f
-› 1 0 -›
III a) Zentrische Streckung um O: x' = 3( )·x
0 1
-› 1 1 0 -›
Umkehrabbildung: x' = -( )·x
3 0 1
b) Zentische Streckung um Z(3|2) mit Streckfaktor -3:
——› 1 0 -› 12
x' = -3( )·x + ( )
0 1 8
——› 1 1 0 -› 4
Umkehrabbildung: x' = - -( )·x + ( )
3 0 1 8/3
--› 4 3 -› 2
c) Ähnlichkeitsabbildung: x' = ( )·x + ( ).
-3 4 2
--› 1 4 -3 -› 1 2
Umkehrabbildung: x' = ——( )·x - - ( ).
25 3 4 25 14
-› 1 2 -›
IV a) Scherung: x' = ( )·x
0 1
-› 1 -2 -›
Umkehrabbildung: x' = ( )·x
0 1
-› 1 0 -›
b) senkrechte Parallelprokektion: x' = ( )x
0 a/b
-› 1 0 -›
Umkehrabbildung: x' = ( )·x
0 b/a
II Beispiele für Kongruenzen im R2
-› a c -› e
Hinweis: Die Schreibweise x' = ( )·x + ( ) bedeutet
b d f
-› x1 -› x1'
für x = ( ) und x' = ( ) :
x2 x2'
———————————————————————
| x1' = a·x1 + c·x2 + e |
| |
| x2' = b·x1 + d·x2 + f |
——————————————————————
a c
Die Koeffizienten der "Matrix" ( ) und der
b d
e
Vektor ( ) ergeben sich aus der Beziehung
f
-› -› -› -› -› -› ——› -› -›
e' = a·e + b·e , e' = c·e + d·e und OO' = e·e + f·e
1 1 2 2 1 2 1 2
-› 1 -› 0
Im Normalfall ist e = ( ), e = ( ) und
1 0 2 1
-› a -› c ——› e
damit e' = ( ), e' = ( ) sowie OO' = ( ).
1 b 2 d f
a) Punktspiegelung an O(0|0)
——› -1
e' = ( ) (erste Zeile ...
1 0
a c
...der Matrix ( )
b d
——› 0
e' = ( ) (zweite Zeile ...
2 -1
-› a c -› -› -1 0 -›
x' = ( )x , also x' = ( )x .
b d 0 -1
Zum Beispiel A(1|1)-›A'(-1|-1),
B(4|0)-›B'(-4|0) und C(3|2)-›C'(-3|-2).
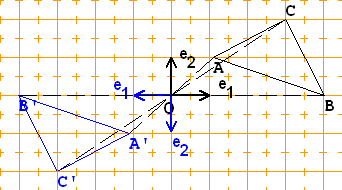
b) Punktspiegelung an O(3|2)
Dieselbe Matrix wie bei a)
——› ——›
e' und e' bestimmen allein die Matrix
1 2
Dazu kommt der "Verschiebungsvektor"
e ——› 6
( ) = OO' = ( )
f 4
-› -1 0 -› 6
x' = ( )x + ( )
0 -1 4
Zum Beispiel: A(4|4)-›A'(2|0),
B(2|4)-›B'(4|0) und C'(3|3)-›C'(3|1)
c)Drehung um den Ursprung mit dem Winkel α = 30°.
cos(α) -sin(α)
e' = ( ) e' = ( )
1 sin(α) 2 cos(α)
Also sind die Abbildungsgleichungen
——› cos(α) - sin(α) -›
x' = ( )x
sin(α) + cos(α)
Für α = 30° also
——› 0,866 - 0,5 -›
x' = ( )x
0,5 0,866
Zum Beispiel A(4|2,5) -› A'(2,21|4,17)
B(7|1,5) -› B'(4,81|5,67)
C(6|6) -› C'(2,20|8,20)
d) Drehung:
Drehwinkel: α = 30° um Drehzentrum Z(3|2).
Diese Drehung kann man sich vorstellen als
Verkettung der folgenden Abbildungen
Parallelverschiebung Z-›O:
-› -› -› -› 3
x = x - b mit b = ( )
1 2
-› -›
Drehung um O (siehe Beispiel c) x = M·x
2 1
cos(α) - sin(α)
mit M = ( )
sin(α) + cos(α)
-› -› -›
und Verschiebung O-›Z x' = x + b
2
-› -› -› -› -› -› -›
Somit x' = M·(x - b ) + b = M·x + b - M·b
-› -› 3 0,866 - 0,5 3
Mit b - M·b = ( ) - ( )·( )
2 0,5 0,866 2
1,401
= ( ) also
-1,232
————————————————————————————————————
| -› 0,866 - 0,5 -› 1,401 |
| x' =( )·x + ( ) |
| 0,5 0,866 -1,232 |
————————————————————————————————————
Beispiel: A(4|2) -› A'(3,867|2,5)
B(6|3) -› B'(5,098|4,366)
C(5|5) -› C'(3,232|5,598)
III Beispiele zur Ähnlichkeitsabbildungen
a) Zentrische Streckung.
Zentrum O. Streckfaktor 3.
-› 3 0 -›
x' = ( )·x Zum Beispiel:
0 3
A(1|1) -› A'(3|3)
B(4|0,5) -› B'(12|1,5)
C(3|1,5) -› C'(9|4,5)
>
b) Zentische Streckung mit Zentrum Z(3|2)
und Streckfaktor k = -3.
-› a -3 -› c 0
e -› ( ) = ( ), e -› ( ) = ( )
1 b 0 2 d -3
——› e 12
OO' = ( ) = ( ). Die Abbildungsgleichung ist
f 8
——› -3 0 -› 12
demnach: x' = ( )·x + ( )
0 -3 8
Zum Beispiel: A(0,5|2,5)-› A'(10,5|0,5)
B(1,5|2) -› B'(7,5|2)
C(1,5|3) -› C'(7,5|-1)
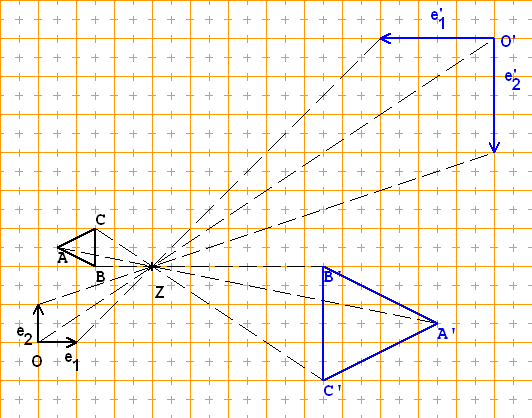
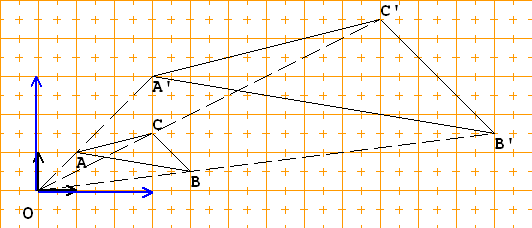
c) Die Ähnlichkeitsabbildung, mit
——› 4 ——› 3
e' = ( ) und e' = ( )
1 -3 2 4
——› e 2
OO' = ( ) = ( ).
f 2
Diese Affinität ist eine Ähnlichkeitsabbildung,
——› --›
da e' und e' senkrecht aufeinander stehen
1 2
und die gleiche Länge 5 haben.
——› 4 3 -› 2
x' = ( )·x + ( ) . Zum Beispiel:
-3 4 2
A(0,5|0,5) -› A'(5,5|2,5)
B(1|0,5) -› B'(7,5|1)
C(0,5|1) -› C'(7|4,5)
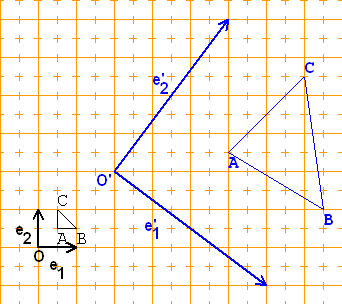
Diese Abbildung kann man sich als Verkettung
einer Drehung um O(0|0) mit 36,87°,
einer zentrischen Streckung um O(0|0 mit
dem Streckfaktor 5 und einer
2
Parallelverschiebung um ( ) vorstellen.
2
IV Beispiel einer affinen Abbildung, ...
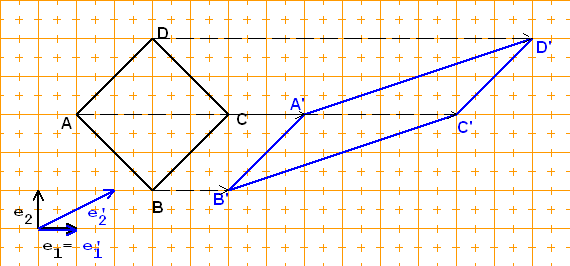
... die weder eine Kongruenzabbildung noch eine Ähnlichkeitsabbild ist.a) Die Scherung, welche die Rechtsachse fest lässt
mit E (1|0) -› E'(1|0)
1 1
und E (0|1) -› E'(2|1)
2 2
-› 1 2 -›
x' = ( )·x zum Beispiel
0 1
A(1|3) -› A'(7|3)
B(3|1) -› B'(5|1)
C(5|3) -› C'(11|3)
D(3|5) -› D'(13|5)
B "wandert um 2 nach rechts",
A und C "wandern um 6 nach recht",
D "wandert um 10 nach rechts":
Je größer der Abstand von der x-Achse
um so größer die "Wanderung".
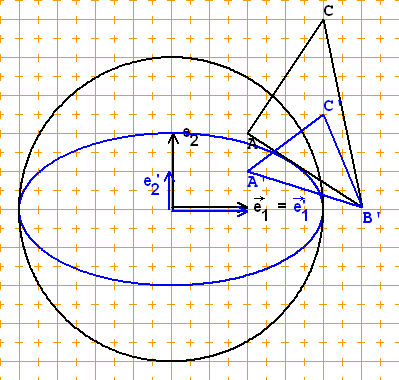
b) Die senkrechte Parallelprojektion,
welche die Rechtsachse fest lässt
mit E (1|0) -› E'(1|0)
1 1
1
und E (0|1) -› E'(0|-)
2 2 2
-› 1 0 -›
x' = ( )·x zum Beispiel
0 1/2
A(1|1) -› A'(1|1/2)
B(2 1/2|0) -› B'(2 1/2|0)
C(2|2 1/4) -› C'(2|1 1/8)
Die Punkte wandern senkrecht zur
x-Achse. Der Abstand halbiert sich.
Aus einem Kreis wird eine Ellipse.
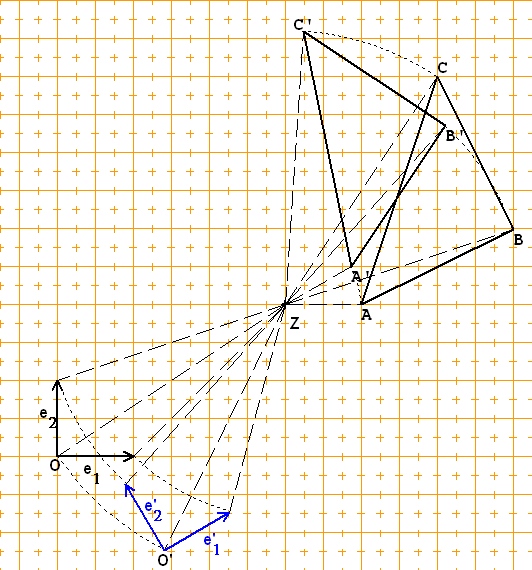
V Koordinatentransformationen in R2
Koordinatentransformationen hängen eng mit Affinitäten zusammen:Betrachtet man die Affinität, die das Koordinatensystem (0,E1,E2) auf das Koordinatensystem (O',E'1,E'2) abbildet, dann ist die Abbildungsgleichung, welche die Koordinaten eines Punktes im zweiten Koordinatensystem aus den Koordinaten des ersten Koordinatensystems berechnet, gerade die Umkehrabbildung dieser Affinität.
-› a -› c
Sei mit O'(e|f) und e' = ( ) und e' = ( )
1 b 2 d
ein zweites Koordinatensystem festgelegt.
Dann gilt für die Koordinaten (x'|x') von P(x |y )
1 2 1 1
-› -›
bezüglich des Koordinatensystems (O',e',e')
1 2
——› ——› -› -› ——›
die Beziehung e' x' + e' x' = e x + e x - OO'
1 1 2 2 1 1 2 2
——› x1'
Mit mit x' = ( ) berechnet sich auf das erste
x2'
a c x1' x1 e
Koordinatensystem bezogen: ( )( ) = ( ) - ( ),
b d x2' x2 f
a c -› -› e -› x1
also ( )·x' = x - ( ) mit x = ( )
b d f x2
x1' -› -›
Achtung: ( ) sind keine Koordinaten bez. (0, e ,e )!
x2' 1 2
a' c' 1 d -c
Sei ( ) = ——————·( ) die inverse Matrix,
b' d' ad -bc -b a
—————————————————————————————
| ——› a' c' -› a' c' e |
dann folgt | x' = ( )x - ( )·( )|
| b' d' b' d' f |
—————————————————————————————
Diese Abbildungsgleichungen sind formal dieselben,
wie die Umkehrabbildung der Affinität f,
-› -› -› -›
die (0, e , e ) auf (O',e' ,e' ) abbildet.
1 2 1 2
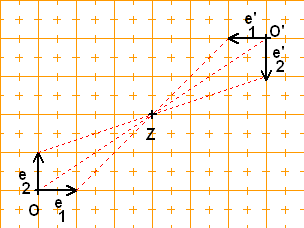
Der Punkt Q(4|5) (siehe rechts) wird
auf P(12|5) abgebildet. Also ist Q(4|5)
das Urbild von f.
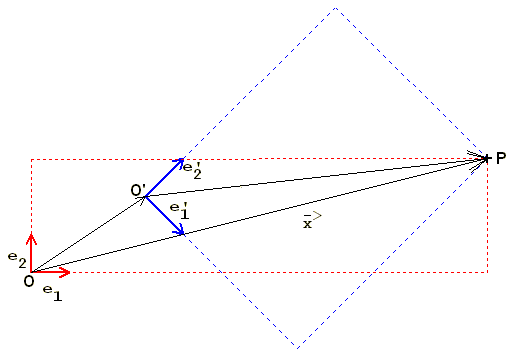
a c 1 1 e 3 a' c' 0,5 0,5
Hier: ( ) = ( ) und ( ) =( ) Mit ( ) = ( )
b d -1 1 f 2 b' d' -0,5 0,5
-› 0,5 -0,5 -› -0,5
folgt: x' = ( )·x + ( )
0,5 0,5 -2,5
Zum Beispiel hat P(12|3) im zweiten Koordinatensystem
0,5 -0,5 12 -0,5 4
die Koordinaten ( )·( ) + ( ) = ( )
0,5 0,5 3 -2,5 5
Somit P(12|5)=
PKoordinaten bezogen auf das zweite System(4|5).
——› -› -› ———› -› -›
Das bedeutet OP = 12e + 5e und O'P = 4e' + 5e' .
1 2 1 2
Affinitäten im R3
I Allgemein
Ähnlich wie im zweidimensionalen Fall, erhält man
die Abbildungsvorschrift der Affinität
|a d g| |j|
-› | | -› | |
x' = |b e h|·x + |k| aus
| | | |
|c f i| |l|
|a| |d| |g| |j|
-› | | -› | | -› | | ——› | |
e' = |b|, e' = |e|, e' = |h| und OO' = |k|.
1 | | 2 | | 3 | | | |
|c| |f| |i| |l|
-› -› -›
[Die Koordinaten bezogen auf (O, e ,e , e ).]
1 2 3
Die Multiplikation der Matrix mit einem Vektor ist
|a d g| |x1| |ax1 + dx2 + gx3|
| | | | | |
definert als |b e h|·|x2| = |bx1 + ex2 + hx3|
| | | | | |
|c f i| |x3| |cx1 + fx2 + ix3|
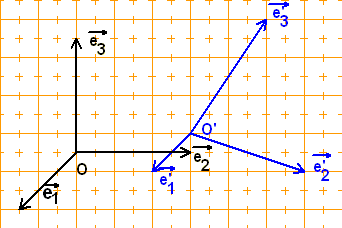
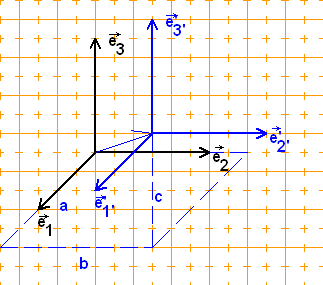
Die Affinität ist eine Ähnlichkeitsabbildung -› -› -› wenn die Vektoren e' , e und e' gleich lang 1 2 3 sind und paarweise senkrecht aufeinander stehen. Haben diese Vektoren zudem die Länge 1, handelt es sich um eine Kongruenzabbildung.
II Beispiele für Kongruenzabbildungen im R3
a) Translation (Parallelverschiebung)
|a|
-› -› | |
Abbildungsgleichung: x' = x + |b|
| |
|c|
|5|
-› -› | |
Hier: x' = x + |4|
| |
|3|
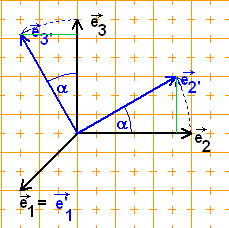
b) Rotation um die x -Achse:
1
|1| | 0 | | 0 |
-› | | --› | | -›| |
e' = |0|, e' = |cos(α)|, e' = |-sin(α)|
1 | | 2 | | 3 | |
|0| |sin(α)| | cos(α)|
|1 0 0 |
-› | | -›
Abbildungsgleichung: x' = |0 cos(α) -sin(α)|·x
| |
|0 sin(α) cos(α) |
Analog leitet man die folgenden zwei Abbildungsgleichungen her:
c) Rotation um die x -Achse
2
|cos(β) 0 sin(β)|
-› | | -›
x' = | 0 1 0 |·x
| |
|-sin(β) 0 cos(β)|
d) Rotation um die x -Achse:
3
|cos(γ) -sin(γ) 0 |
| | -›
= |sin(γ) cos(γ) 0 |·x
| |
| 0 0 1 |