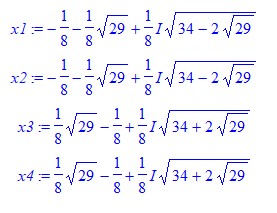Die Homepage von Joachim Mohr
Neu 2023: Formeln zur Lösung der Gleichungen 3. und 4. Grades
kubische Gleichung ... Gleichungen 4. Grades
Höhere Mathematik
In der Schule löst man quadratische Gleichungen.
Hier die Formel für Gleichunge 3. une 4. Grades.
- TTMathe rechnet vor
- Die reduzierte kubische Gleichung
- Die kubische Gleichung
- Die Gleichung 4. Grades
- Sonderfälle der kubischen Gleichung
- Sonderfälle der Gleichung 4. Grades
- Die Gleichung 4. Grades, Formel von Joachim Mohr
Die reduzierte kubische Gleichung
x3 + px + q = 0
Berechnung von Beispielen
Im Folgenden sprechen wir von der Formel von Cardano, der diese Formel
als erster publiziert hat. Der Erste, der eine Formel für die Gleichung 3. Ordnung fand, war Scipio del Ferro, der sie seinem Schüler Fiore und seinem Schwiegersohn vor seinem Tod mitteilte. Bei einem mathematischen Wettstreit mit Fiore fand Niccolo Fontana, genannt TARTAGLIA ("Stotterer"), ebenfalls die Lösung. Cardano gelang durch Substitution die Überführung der allgemeinen kubischen Gleichung in die reduzierte Form.
Ferrari, einem Schüler Cardanos, gelang dann die Lösung der allgemeinen quartischen, also der Gleichung vierter Ordnung.
Die Lösung der kubischen Gleichung x3 + px + q = 0 ist nach Cardano:
3 q 3 q
x=u+v für u = - - + sqrt(d) und v = - - - sqrt(d).
2 2
q 2 p 3 p
mit d = (-) + (-) und der Nebenbedingung u·v= - -.
2 3 3
Hinweis: +sqrt(d) und -sqrt(d) sind die beiden (komplexen) Quadratwurzeln von d.
Für u und v gibt es jeweils drei Lösungen als (komplexe) Kubikwurzel.
Mit der angegebenen Nebenbedingung gibt es dann genau drei Lösungen der kubischen Gleichung.
Für u und v gibt es jeweils drei Lösungen als (komplexe) Kubikwurzel.
Mit der angegebenen Nebenbedingung gibt es dann genau drei Lösungen der kubischen Gleichung.
Rechenschema:
Hinweis: cis(α) = cos(α) + i·sin(α)
Die drei Lösungen von x3 = 1 sind 1, cis(120°) und cis(240°).
Ist u1 eine dritte Wurzel von x3 = a, dann sind die beiden anderen
u2 = u1·cis(120°) und u3 = u1·cis(240°).
p=... q=... (Werte einsetzten!) d=(q/2)^2+(p/3)^3 Bedeutung: uc=u^3 vc=v^3 uc=-q/2+d^(1/2) vc=-q/2-d^(1/2) u1=uc^(1/3) u2=u1*cis(120°) u3=u1*cis(240°) v1=vc^(1/3) v2=v1*cis(120°) v3=v1*cis(240°) Suche ein u und ein v mit u*v=-p/3! u=u2 (zum Beispiel) v=v2 (zum Beispiel) u*v (berechnen) -p/3 (berechnen und überprüfen: ist u*v=-p3?) x1=u+v x2=u*cis(120°)+v*cis(240°) x3=u*cis(240°)+v*cis(120°)Kann so direkt mit TTMathe (Rechenblatt für komplexe Zahlen) gerechnet werden.
Herleitung der Formel von Cardano: Setze x=u+v
3 2 2 3
=> u + 3u v + 3uv + v + p(u+v)+q = 0
3 3
=> u + 3uv(u+v) + v + p(u+v)+q = 0
3 3
=> u + (3uv+p)·(u+v) +v +q = 0
3 3
Mit 3uv+p=0 (*) (kann gesetzt werden) folgt: u + v = -q (**)
6 3 3 6 2 3 3 4 3
(**)=> u + 2u ·v + v = q (*) => 4u ·v = - —— p
27
6 3 3 6 2 4 3
Subtraktion: u - 2u ·v + v = q + —— p
24
3 3 2 q 2 p 3
d.h (u - v ) = 4·d für d=(-) +(-) (***)
2 3
3 3
Somit gilt: u + v = -q
3 3
u - v = 2sqrt(d)
3 q
Summe/2 u = - - + sqrt(d)
2
3 q
Differenz/2 v = - - - sqrt(d)
2
Literatur: Gregor Milla (Gammertingen):Gleichungen dritten und vierten Grades.
I) Beispiel für d ≤ 0 (Casus irreducibilis)
In diesem Fall gibt es stets drei reelle Lösungen.Alle Beispiele gerechnet mit TTMathe (Rechenblatt für komplexe Zahlen)
Hinweis: cis(α) = cos(α) + i*sin(α)
a) x3 - 3x + 2 = 0
p=-3
q=2
d=(q/2)^2+(p/3)^3=0
Bedeutung: uc=u^3 vc=v^3
uc=-q/2+d^(1/2)=-1
vc=-q/2-d^(1/2)=-1
u1=uc^(1/3)=1/2+1/2*sqrt(3)i=0,5+0,866i=cis(60°)
u2=u1*cis(120°)=-1
u3=u1*cis(240°)=1/2-1/2*sqrt(3)i=0,5-0,866i=cis(300°)
v1=vc^(1/3)=1/2+1/2*sqrt(3)i=0,5+0,866i=cis(60°)
v2=v1*cis(120°)=-1
v3=v1*cis(240°)=1/2-1/2*sqrt(3)i=0,5-0,866i=cis(300°)
Suche passende u und v mit u*v=-p/3
(Dies sieht sofort an der Winkelsumme.)
Die passenden gefunden:
u1*v3=1
u2*v2=1
u3*v1=1
Drei reelle Lösungen:
x1=u1+v3=1
x2=u2+v2=-2
x3=u3+v1=1
x1=u1+v3=1
x2=u2+v2=-2
x3=u3+v1=1
3 7 20
b) x - -x + —— = 0
3 27
p=-7/3
q=20/27
d=(q/2)^2+(p/3)^3=-1/3
Bedeutung: uc=u^3 vc=v^3
uc=-q/2+d^(1/2)=(-10/27)+1/3*sqrt(3)i =-0,37+0,577i=7/27*sqrt(7)*cis(122,68°)
vc=-q/2-d^(1/2)=(-10/27)-1/3*sqrt(3)i =-0,37-0,577i=7/27*sqrt(7)*cis(237,32°)
u1=uc^(1/3)=2/3+1/3*sqrt(3)i=0,667+0,577i =1/3*sqrt(7)*cis(40,89°)
u2=u1*cis(120°)=(-5/6)+1/6*sqrt(3)i =-0,833+0,289i=1/3*sqrt(7)*cis(160,89°)
u3=u1*cis(240°)=1/6-1/2*sqrt(3)i =0,167-0,866i=1/3*sqrt(7)*cis(280,89°)
v1=vc^(1/3)=1/6+1/2*sqrt(3)i =0,167+0,866i=1/3*sqrt(7)*cis(79,11°)
v2=v1*cis(120°)=(-5/6)-1/6*sqrt(3)i =-0,833-0,289i=1/3*sqrt(7)*cis(199,11°)
v3=v1*cis(240°)=2/3-1/3*sqrt(3)i =0,667-0,577i=1/3*sqrt(7)*cis(319,11°)
Suche passende u und v mit u*v=-p/3
Die passenden gefunden:
u1*v3=7/9
u2*v2=7/9
u3*v1=7/9
Drei reelle Lösungen:
x1=u1+v3=4/3=1,333
x2=u2+v2=-5/3=-1,667
x3=u3+v1=1/3=0,333
x1=u1+v3=4/3=1,333
x2=u2+v2=-5/3=-1,667
x3=u3+v1=1/3=0,333
c) x3 - 7x - 6 = 0
p=-7
q=-6
d=(q/2)^2+(p/3)^3=-100/27
Bedeutung: uc=u^3 vc=v^3
uc=-q/2+d^(1/2)=3+10/9*sqrt(3)i =3+1,925i=7/9*sqrt(21)*cis(32,68°)
vc=-q/2-d^(1/2)=3-10/9*sqrt(3)i =3-1,925i=7/9*sqrt(21)*cis(327,32°)
u1=uc^(1/3)=3/2+1/6*sqrt(3)i =1,5+0,289i=1/3*sqrt(21)*cis(10,89°)
u2=u1*cis(120°)=(-1)+2/3*sqrt(3)i =-1+1,155i=1/3*sqrt(21)*cis(130,89°)
u3=u1*cis(240°)=(-1/2)-5/6*sqrt(3)i =-0,5-1,443i=1/3*sqrt(21)*cis(250,89°)
v1=vc^(1/3)=(-1/2)+5/6*sqrt(3)i =-0,5+1,443i=1/3*sqrt(21)*cis(109,11°)
v2=v1*cis(120°)=(-1)-2/3*sqrt(3)i =-1-1,155i=1/3*sqrt(21)*cis(229,11°)
v3=v1*cis(240°)=3/2-1/6*sqrt(3)i =1,5-0,289i=1/3*sqrt(21)*cis(349,11°)
Suche passende u und v mit u*v=-p/3
Die passenden gefunden:
u1*v3=7/3
u2*v2=7/3
u3*v1=7/3
Drei reelle Lösungen:
x1=u1+v3=3
x2=u2+v2=-2
x3=u3+v1=-1
x1=u1+v3=3
x2=u2+v2=-2
x3=u3+v1=-1
d) x3 - 5x - 2 = 0
p=-5
q=-2 #d=(q/2)^2+(p/3)^3=-98/27
Bedeutung: uc=u^3 vc=v^3
uc=-q/2+d^(1/2)=1+7/9*sqrt(6)i =1+1,905i=5/9*sqrt(15)*cis(62,31°)
vc=-q/2-d^(1/2)=1-7/9*sqrt(6)i =1-1,905i=5/9*sqrt(15)*cis(297,69°)
u1=uc^(1/3)=(1/2+1/2*sqrt(2))+(1/2*sqrt(3)-1/6*sqrt(6))*i =1,207+0,458i=1/3*sqrt(15)*cis(20,77°)
u2=u1*cis(120°)=(-1)+1/3*sqrt(6)i =-1+0,816i=1/3*sqrt(15)*cis(140,77°)
u3=u1*cis(240°)=(-1/2*sqrt(2)+1/2)+(-1/2*sqrt(3)-1/6*sqrt(6))*i =-0,207-1,274i=1/3*sqrt(15)*cis(260,77°)
v1=vc^(1/3)=(-1/2*sqrt(2)+1/2)+(1/2*sqrt(3)+1/6*sqrt(6))*i =-0,207+1,274i=1/3*sqrt(15)*cis(99,23°)
v2=v1*cis(120°)=(-1)-1/3*sqrt(6)i=-1-0,816i =1/3*sqrt(15)*cis(219,23°)
v3=v1*cis(240°)=(1/2+1/2*sqrt(2))+(-1/2*sqrt(3)+1/6*sqrt(6))*i =1,207-0,458i=1/3*sqrt(15)*cis(339,23°)
Suche passende u und v mit u*v=-p/3
Die passenden gefunden:
u1*v3=5/3
u2*v2=5/3
u3*v1=5/3
Drei reelle Lösungen:
x1=u1+v3=1+sqrt(2)=2,414
x2=u2+v2=-2
x3=u3+v1=-sqrt(2)+1=-0,414
x1=u1+v3=1+sqrt(2)=2,414
x2=u2+v2=-2
x3=u3+v1=-sqrt(2)+1=-0,414
II) Beispiele für d > 0 (Casus reducibilis)
In diesem Fall gibt es stets eine reelle Lösung und zwei komplexe lösungen.
a) x3 - 2x + 4 = 0
p=-2
q=4
d=(q/2)^2+(p/3)^3=100/27
Bedeutung: uc=u^3 vc=v^3
uc=-q/2+d^(1/2)=-2+10/9*sqrt(3)=-0,075
vc=-q/2-d^(1/2)=-2-10/9*sqrt(3)=-3,925
u1=uc^(1/3)=(1/2-1/6*sqrt(3))+(1/2*sqrt(3)-1/2)*i=0,211+0,366i=1-1/3*sqrt(3)*cis(60°)
u2=u1*cis(120°)=-1+1/3*sqrt(3)=-0,423
u3=u1*cis(240°)=(1/2-1/6*sqrt(3))+(-1/2*sqrt(3)+1/2)*i=0,211-0,366i=1-1/3*sqrt(3)*cis(300°)
v1=vc^(1/3)=(1/2+1/6*sqrt(3))+(1/2+1/2*sqrt(3))*i=0,789+1,366i=1+1/3*sqrt(3)*cis(60°)
v2=v1*cis(120°)=-1-1/3*sqrt(3)=-1,577
v3=v1*cis(240°)=(1/2+1/6*sqrt(3))+(-1/2-1/2*sqrt(3))*i=0,789-1,366i=1+1/3*sqrt(3)*cis(300°)
Suche passende u und v mit u*v=-p/3
Die passenden gefunden:
u1*v3=2/3
u2*v2=2/3
u3*v1=2/3
Eine reelle und zwei komplexe Lösungen:
x1=u1+v3=1-i
x2=u2+v2=-2
x3=u3+v1=1+i
x1=u1+v3=1-i
x2=u2+v2=-2
x3=u3+v1=1+i
3 1 5
b) x + -x - - = 0
4 4
p=1/4
q=-5/4
d=(q/2)^2+(p/3)^3=169/432
Bedeutung: uc=u^3 vc=v^3
uc=-q/2+d^(1/2)=5/8+13/36*sqrt(3)=1,25046
vc=-q/2-d^(1/2)=-6755/14596202=-0,00046
u1=uc^(1/3)=1/2+1/3*sqrt(3)=1,07735
u2=u1*cis(120°)=(-1/4-1/6*sqrt(3))+(1/2+1/4*sqrt(3))*i =-0,53868+0,93301i=1/2+1/3*sqrt(3)*cis(120°)
u3=u1*cis(240°)=(-1/4-1/6*sqrt(3))+(-1/2-1/4*sqrt(3))*i =-0,53868-0,93301i=1/2+1/3*sqrt(3)*cis(240°)
v1=vc^(1/3)=263445/6811741+(1/2-1/4*sqrt(3))*i =0,03868+0,06699i=1/3*sqrt(3)-1/2*cis(60°)
v2=v1*cis(120°)=-1/3*sqrt(3)+1/2=-0,07735
v3=v1*cis(240°)=263445/6811741+(-1/2+1/4*sqrt(3))*i =0,03868-0,06699i=1/3*sqrt(3)-1/2*cis(300°)
Suche passende u und v
(Winkel zusammen 360°)
(oder u*v=-p/3)
Die passenden gefunden:
u1*v2=-1/12
u2*v1=-1/12
u3*v3=-1/1
Eine reelle Lösung und zwei komplexe Lösungen:
x1=u1+v2=1
x2=u2+v1=(-1/2)+i
x3=u3+v3=(-1/2)-i
x1=u1+v2=1
x2=u2+v1=(-1/2)+i
x3=u3+v3=(-1/2)-i
c) x3 + 2x + 3 = 0
p=2
q=3
d=(q/2)^2+(p/3)^3=275/108
Bedeutung: uc=u^3 vc=v^3
uc=-q/2+d^(1/2)=-3/2+5/18*sqrt(33)=0,096
vc=-q/2-d^(1/2)=-3/2-5/18*sqrt(33)=-3,096
u1=uc^(1/3)=1/6*sqrt(33)-1/2=0,457
u2=u1*cis(120°)=(-1/12*sqrt(33)+1/4)+(1/4*sqrt(11)-1/4*sqrt(3))*i =-0,229+0,396i=1/6*sqrt(33)-1/2*cis(120°)
u3=u1*cis(240°)=(-1/12*sqrt(33)+1/4)+(-1/4*sqrt(11)+1/4*sqrt(3))*i =-0,229-0,396i=1/6*sqrt(33)-1/2*cis(240°)
v1=vc^(1/3)=(1/4+1/12*sqrt(33))+(1/4*sqrt(3)+1/4*sqrt(11))*i =0,729+1,262i=1/2+1/6*sqrt(33)*cis(60°)
v2=v1*cis(120°)=-1/2-1/6*sqrt(33)=-1,457
v3=v1*cis(240°)=(1/4+1/12*sqrt(33))+(-1/4*sqrt(3)-1/4*sqrt(11))*i =0,729-1,262i=1/2+1/6*sqrt(33)*cis(300°)
Suche passende u und v
(Winkel zusammen 360°)
(oder u*v=-p/3)
Die passenden gefunden:
u1*v2=-2/3=-0,667
u2*v1=-2/3=-0,667
u3*v3=-2/3=-0,667
Eine reelle Lösung und zwei komplexe Lösungen:
x1=u1+v2=-1
x2=u2+v1=1/2+1/2*sqrt(11)i
x3=u3+v3=1/2-1/2*sqrt(11)i
x1=u1+v2=-1
x2=u2+v1=1/2+1/2*sqrt(11)i
x3=u3+v3=1/2-1/2*sqrt(11)i
Ein Beispiel, bei dem TTMathe keine Wurzelausdrücke findet:
d) x3 + 7x + 11 = 0
p=7
q=11
d=(q/2)^2+(p/3)^3=4639/108=42,9537037037037037
Bedeutung: uc=u^3 vc=v^3
uc=-q/2+d^(1/2)=1,05390751412496694
vc=-q/2-d^(1/2)=-12,0539075141249669
u1=uc^(1/3)=1,01765561605588337
u2=u1*cis(120°)=4639/108 =-0,508827808027941685+0,88131561580829806i =1,01765561605588337*cis(120°)
u3=u1*cis(240°)=4639/108 =-0,508827808027941685-0,88131561580829806i =1,01765561605588337*cis(240°)
v1=vc^(1/3)=4639/108 =1,14642581268140963+1,985667754672642i =2,29285162536281926*cis(60°)
v2=v1*cis(120°) =-2,29285162536281926
v3=v1*cis(240°) =1,14642581268140963-1,985667754672642i =2,29285162536281926*cis(300°)
Suche passende u und v
(Winkel zusammen 360°)
(oder u*v=-p/3)
Die passenden gefunden:
u1*v2=-7/3=-2,33333333333333333
u2*v1=-7/3=-2,33333333333333333
u3*v3=-7/3=-2,33333333333333333
Eine reelle und zwei komplexe Lösungen:
x1=u1+v2 =-1,27519600930693589
x2=u2+v1 =0,637598004653467947 +2,86698337048094006i =2,9370265341246638*cis(77,46°)
x3=u3+v3 =0,637598004653467946 -2,86698337048094006i =2,9370265341246638*cis(282,54°)
Probe
x1=u1+v2 =-1,27519600930693589
x2=u2+v1 =0,637598004653467947 +2,86698337048094006i =2,9370265341246638*cis(77,46°)
x3=u3+v3 =0,637598004653467946 -2,86698337048094006i =2,9370265341246638*cis(282,54°)
x1^3+p*x1+q=0=0,000000000000000003
x2^3+p*x2+q=0=-0,000000000000000003
x3^3+p*x3+q=0=0,000000000000000001
Die kubische Gleichung
ax3 + bx2 + cx + d = 0
Sonderfälle der allgemeinen kubischen Gleichung
Die kubischen Gleichung wird durch die Substition von x=z-b/(3·a) auf die reduzierte kubische Gleichung z3 + pz + q = 0 zurückgeführt mit:
b c 1 b 2 2 b 3 1 b c d
x = z - —— , p = - - -·(-) und q = ——·(-) - -·-·- + -
3a a 3 a 27 a 3 a a a
Rechenschema: a= ... b= ... c= ... d= ... p=c/a-(b/a)^2/3 q=2/27*(b/a)^3-1/3*(b/a)*(c/a)+d/a Lösung von x^3 + px + q = 0 nach Cardano dd=(q/2)^2+(p/3)^3 Bedeutung: uc=u^3 vc=v^3 uc=-q/2+dd^(1/2) vc=-q/2-dd^(1/2) u1=uc^(1/3) u2=u1*cis(120°) u3=u1*cis(240°) v1=vc^(1/3) v2=v1*cis(120°) v3=v1*cis(240°) Suche zu einander passende u und v mit u*v=-p/3! Mit z=u+v (drei Lösungen) erhält man durch Resubstitution die Lösung x=z-b/(3a) (drei Lösungen)
Beispiele zur kubischen Gleichung
Gerechnet mit TTMathe (Rechenblatt für komplexe Zahlen).
a) 9x3 - 43x2 + 145x - 91 = 0
a=9
b=-43
c=145
d=-91
Subst. x=z-b/(3*a)
p=c/a-(b/a)^2/3=2066/243
q=2/27*(b/a)^3-1/3*(b/a)*(c/a)+d/a=7,468576945
Lösung von x^3 + px + q = 0 nach Cardano
dd=(q/2)^2+(p/3)^3=36,706802825
Bedeutung: uc=u^3 vc=v^3
uc=-q/2+dd^(1/2)=2,324325464
vc=-q/2-dd^(1/2)=-9,792902408
u1=uc^(1/3)=sqrt(3)-11/27=1,3246434
u2=u1*cis(120°)=(-1/2*sqrt(3)+11/54)+(3/2-11/54*sqrt(3))*i =-0,6623217+1,147174835i=sqrt(3)-11/27*cis(120°)
u3=u1*cis(240°)=(-1/2*sqrt(3)+11/54)+(-3/2+11/54*sqrt(3))*i =-0,6623217-1,147174835i=sqrt(3)-11/27*cis(240°)
v1=vc^(1/3)=(1/2*sqrt(3)+11/54)+(3/2+11/54*sqrt(3))*i =1,069729107+1,852825165i=sqrt(3)+11/27*cis(60°)
v2=v1*cis(120°)=-sqrt(3)-11/27=-2,139458215
v3=v1*cis(240°)=(1/2*sqrt(3)+11/54)+(-3/2-11/54*sqrt(3))*i =1,069729107-1,852825165i=sqrt(3)+11/27*cis(300°)
Suche zu einander passende u und v so mit u*v=-p/3!
Die passenden gefunden:
-p/3=-2066/729=-2,834019204
u1*v2=-2066/729=-2,834019204
u2*v1=-2066/729=-2,834019204
u3*v3=-2066/729=-2,834019204
z1=u1+v2=-22/27=-0,814814815
z2=u2+v1=11/27+3i=0,407407407+3i =1/27*sqrt(6682)*cis(82,27°)
z3=u3+v3=11/27-3i=0,407407407-3i =1/27*sqrt(6682)*cis(277,73°)
Resubstitution
x1=z1-b/(3*a)=7/9
x2=z2-b/(3*a)=2+3i=2+3i
x3=z3-b/(3*a)=2-3i=2-3i
Somit eine reelle und zwei komplexe Lösungen:
x1=7/9
x2=2+3i
x3=2-3i
x1=7/9
x2=2+3i
x3=2-3i
b) 8x3 + 4x2 - 4x -1 = 0
Siehe Konstruktion des Siebenecks
a=8
b=4
c=-4
d=-1
Subst. x=z-b/(3*a)
p=c/a-(b/a)^2/3=-7/12=-0,583333333
q=2/27*(b/a)^3-1/3*(b/a)*(c/a)+d/a=-7/216=-0,032407407
Lösung von x^3 + px + q = 0
nach Cardano
dd=(q/2)^2+(p/3)^3=-49/6912=-0,00708912
Bedeutung: uc=u^3 vc=v^3
uc=-q/2+dd^(1/2)=7/432+7/144*sqrt(3)i =0,016203704+0,084196914i=7/216*sqrt(7)*cis(79,11°)
vc=-q/2-dd^(1/2)=7/432-7/144*sqrt(3)i =0,016203704-0,084196914i=7/216*sqrt(7)*cis(280,89°)
u1=uc^(1/3)=0,395078234+0,195851049i =1/6*sqrt(7)*cis(26,37°)
u2=u1*cis(120°)=-0,367151101+0,244222263i =1/6*sqrt(7)*cis(146,37°)
u3=u1*cis(240°)=-0,027927134-0,440073312i =1/6*sqrt(7)*cis(266,37°)
v1=vc^(1/3)=-0,027927134+0,440073312i =1/6*sqrt(7)*cis(93,63°)
v2=v1*cis(120°)=-0,367151101-0,244222263i =1/6*sqrt(7)*cis(213,63°)
v3=v1*cis(240°)=0,395078234-0,195851049i =1/6*sqrt(7)*cis(333,63°)
Suche zu einander passende u und v so mit u*v=-p/3!
Die passenden gefunden:
-p/3=7/36=0,194444444
u1*v3=7/36=0,194444444
u2*v2=7/36=0,194444444
u3*v1=7/36=0,194444444
z1=u1+v3=0,790156469
z2=u2+v2=-0,734302201
z3=u3+v1=-0,055854267
Man sieht hier z1 = 2*Realteil(u1)
z2 = 2*Realteil(u2)
z3 = 2*Realteil(u3)
Resubstitution
x1=z1-b/(3*a)=0,623489802
x2=z2-b/(3*a)=-0,900968868
x3=z3-b/(3*a)=-0,222520934
Probe
a*x1^3+b*x1^2+c*x1+d=0
a*x2^3+b*x2^2+c*x2+d=0
a*x3^3+b*x3^2+c*x3+d=0
Somit drei reelle Lösungen:
x1 = 0,623489802
x2 = -0,900968868
x3 = -0,222520934
Nebenbei bemerkt ist (siehe Das Siebeneck)
x1 = 0,623489802
x2 = -0,900968868
x3 = -0,222520934
x1=cos(2/7*Pi)=cos(360°/7) x2=cos(6/7*Pi)=cos(3*360°/7) x3=cos(4/7*Pi)=cos(2*360°/7)
c) x3 - 4x2 - 7x + 22 = 0
a=1
b=-4
c=-7
d=22
wird auf die red. kub. Gl.
z^3+p*z+q=0 zurückgeführt.
Subst. x=z-b/(3*a)
p=c/a-(b/a)^2/3=-37/3
q=2/27*(b/a)^3-1/3*(b/a)*(c/a)+d/a=214/27
Lösung von z^3 + pz + q = 0
nach Cardano
dd=(q/2)^2+(p/3)^3=-484/9=-53,777777778
Bedeutung: uc=u^3 vc=v^3
uc=-q/2+dd^(1/2)=(-107/27)+22/3i =-3,962962963+7,333333333i =37/27*sqrt(37)*cis(118,39°)
vc=-q/2-dd^(1/2)=(-107/27)-22/3i =-3,962962963-7,333333333i =37/27*sqrt(37)*cis(241,61°)
u1=uc^(1/3)=(sqrt(3)-1/6)+(1+1/6*sqrt(3))*i =1,565384141+1,288675135i =1/3*sqrt(37)*cis(39,46°)
u2=u1*cis(120°)=(-sqrt(3)-1/6)+(1-1/6*sqrt(3))*i =-1,898717474+0,711324865i =1/3*sqrt(37)*cis(159,46°)
u3=u1*cis(240°)=1/3-2i=0,333333333-2i =1/3*sqrt(37)*cis(279,46°)
v1=vc^(1/3)=1/3+2i=0,333333333+2i =1/3*sqrt(37)*cis(80,54°)
v2=v1*cis(120°)=(-sqrt(3)-1/6)+(-1+1/6*sqrt(3))*i =-1,898717474-0,711324865i=1/3*sqrt(37)*cis(200,54°)
v3=v1*cis(240°)=(sqrt(3)-1/6)+(-1-1/6*sqrt(3))*i =1,565384141-1,288675135i=1/3*sqrt(37)*cis(320,54°)
Suche zu einander passende u und v so mit u*v=-p/3!
Die passenden gefunden:
-p/3=37/9=4,111111111
u1*v3=37/9=4,111111111
u2*v2=37/9=4,111111111
u3*v1=37/9=4,111111111
z1=u1+v3=2*sqrt(3)-1/3=3,130768282
z2=u2+v2=-1/3-2*sqrt(3)=-3,797434948
z3=u3+v1=2/3=0,666666667
Resubstitution
x1=z1-b/(3*a)=1+2*sqrt(3)=4,464101615
x2=z2-b/(3*a)=-2*sqrt(3)+1=-2,464101615
x3=z3-b/(3*a)=2
Drei reelle Lösungen:
x1 = 1+2*sqrt(3) = 4,464101615
x2 = -2*sqrt(3)+1 = -2,464101615
x3 = 2
x1 = 1+2*sqrt(3) = 4,464101615
x2 = -2*sqrt(3)+1 = -2,464101615
x3 = 2
d) 36x3 - 28x2 - 9x + 7 = 0
a=36
b=-28
c=-9
d=7
Subst. x=z-b/(3*a)
p=c/a-(b/a)^2/3=-439/972=-0,451646091
q=2/27*(b/a)^3-1/3*(b/a)*(c/a)+d/a=3731/39366=0,094777219
Lösung von x^3 + px + q = 0
nach Cardano
dd=(q/2)^2+(p/3)^3=-0,001166492
Bedeutung: uc=u^3 vc=v^3
uc=-q/2+dd^(1/2)=(-3731/78732)+115/5832*sqrt(3)i =-0,047388609+0,034153951i=0,058413806*cis(144,22°)
vc=-q/2-dd^(1/2)=(-3731/78732)-115/5832*sqrt(3)i =-0,047388609-0,034153951i=0,058413806*cis(215,78°)
u1=uc^(1/3)=7/27+1/6*sqrt(3)i =0,259259259+0,288675135i =1/54*sqrt(439)*cis(48,07°)
u2=u1*cis(120°)=(-41/108)+5/108*sqrt(3)i =-0,37962963+0,080187537i =1/54*sqrt(439)*cis(168,07°)
u3=u1*cis(240°)=13/108-23/108*sqrt(3)i =0,12037037-0,368862672i =1/54*sqrt(439)*cis(288,07°)
v1=vc^(1/3)=13/108+23/108*sqrt(3)i =0,12037037+0,368862672i=1/54*sqrt(439)*cis(71,93°)
v2=v1*cis(120°)=(-41/108)-5/108*sqrt(3)i =-0,37962963-0,080187537i =1/54*sqrt(439)*cis(191,93°)
v3=v1*cis(240°)=7/27-1/6*sqrt(3)i =0,259259259-0,288675135i =1/54*sqrt(439)*cis(311,93°)
Suche zu einander passende u und v so mit u*v=-p/3!
Die passenden gefunden:
-p/3=439/2916=0,150548697
u1*v3=439/2916=0,150548697
u2*v2=439/2916=0,150548697
u3*v1=439/2916=0,150548697
z1=u1+v3=14/27=0,518518519
z2=u2+v2=-41/54=-0,759259259
z3=u3+v1=13/54=0,240740741
Resubstitution
x1=z1-b/(3*a)=7/9
x2=z2-b/(3*a)=-1/2
x3=z3-b/(3*a)=1/2
Probe
a*x1^3+b*x1^2+c*x1+d=0
a*x2^3+b*x2^2+c*x2+d=0
a*x3^3+b*x3^2+c*x3+d=0
Somit drei reelle Lösungen:
x1 = 7/9
x2 = -1/2
x3 = 1/2
x1 = 7/9
x2 = -1/2
x3 = 1/2
Die allgemeine Gleichung 4. Grades
ax4 + bx3 + cx2 + dx+e = 0
Siehe auch diesen Lösungsweg (Formel von Joachim Mohr).Die Lösung der Gleichung
ax4 + bx3 + cx2 + dx+e = 0 bzw. x4+A*x3+B*x2+C*x+D=0
für A=b/a B=c/a C=d/a und D=e/a erfolgt in zwei Schritten:
1. Schritt: Löse y3-B/2*y2+1/4*(AC-4*D)*y+1/8*(4BD-A^2*D-C^2)=0
2. Schritt: Löse x2+(A/2+s)*x+(y+t) = 0 und x2+(A/2-s)*x+(y-t)=0
für s=sqrt(1/4*A^2+2*y-B) und t=(Ay-C)/(2s)
bzw. t=sqrt(y^2-D) (falls s=0)
Rechenschema:
ax^4+bx^3-cx^2+dx+e=0
a=... (Werte einsetzten)
b=...
c=...
d=...
e=...
Die kub. Gl. y^3+b1y^2+c1y+d1=0 ...
b1=-c/(2*a)
c1=1/4*(b*d/a-4*e)/a
d1=1/8*(4*c*e-b*b*e/a-d*d)/(a*a)
... wird auf die red. kub. Gl.
z^3+p*z+q=0 zurückgeführt.
Subst. x=z-b/(3*a)
p=c1-b1^2/3
q=2/27*b1^3-1/3*b1*c1+d1
Lösung von z^3 + pz + q = 0
nach Cardano
dd=(q/2)^2+(p/3)^3
Bedeutung: uc=u^3 vc=v^3
uc=-q/2+dd^(1/2)
vc=-q/2-dd^(1/2)
u1=uc^(1/3)
u2=u1*cis(120°)
u3=u1*cis(240°)
v1=vc^(1/3)
v2=v1*cis(120°)
v3=v1*cis(240°)
Suche u und v so mit u*v=-p/3!
Überprüfe ob die folgenden 4 Werte gleich sind:
(Wenn nicht: prüfe u1*v1 bzw. u1*v2 etc. und
rechne mit u1+v1, falls u1+v1 = -p/3 etc.)
-p/3
u1*v3
u2*v2
u3*v1
z1=u1+v3
z2=u2+v2
z3=u3+v1
Resubstitution
y1=z1-b1/3
y2=z2-b1/3
y3=z3-b1/3
Eine Lösung y genügt
y=y1
s=(1/4*(b/a)^2+2*y-c/a)^(1/2)
t=(b/a*y-d/a)/(2*s)
Falls s=0 t=(y^2-e/a)^(1/2)
Zu Lösen bleibt
x^2+r1*x+w1=0 und x^2+r2x+w2=0
r1=b/(2*a)+s
w1=y+t
r2=b/(2*a)-s
w2=y-t
x1=-r1/2+((r1/2)^2-w1)^(1/2)
x2=-r1/2-((r1/2)^2-w1)^(1/2)
x3=-r2/2+((r2/2)^2-w2)^(1/2)
x4=-r2/2-((r2/2)^2-w2)^(1/2)
Beispiele zur Gleichung 4. Grades
a) x4 + x3 + x2 + x + 1=0
a=1
b=1
c=1
d=1
e=1
Die kub. Gl. y^3+b1y^2+c1y+d1=0 ...
b1=-c/(2*a)=-1/2
c1=1/4*(b*d/a-4*e)/a=-3/4
d1=1/8*(4*c*e-b*b*e/a-d*d)/(a*a)=1/4
... wird auf die red. kub. Gl.
z^3+p*z+q=0 zurückgeführt.
Subst. x=z-b/(3*a)
p=c1-b1^2/3=-5/6
q=2/27*b1^3-1/3*b1*c1+d1=25/216
Lösung von z^3 + pz + q = 0
nach Cardano
dd=(q/2)^2+(p/3)^3=-125/6912
Bedeutung: uc=u^3 vc=v^3
uc=-q/2+dd^(1/2)=(-25/432)+5/144*sqrt(15)i =-0,05787037+0,134478588i =5/108*sqrt(10)*cis(113,28°)
vc=-q/2-dd^(1/2)=(-25/432)-5/144*sqrt(15)i =-0,05787037-0,134478588i =5/108*sqrt(10)*cis(246,72°)
u1=uc^(1/3)=5/12+1/12*sqrt(15)i =0,416666667+0,322748612i =1/6*sqrt(10)*cis(37,76°)
u2=u1*cis(120°)=(-1/8*sqrt(5)-5/24)+(sqrt(5/32-5/96*sqrt(5)))*i =-0,487841831+0,199469612i=1/6*sqrt(10)*cis(157,76°)
u3=u1*cis(240°)=(1/8*sqrt(5)-5/24)+(1/24*sqrt(15)+5/24*sqrt(3))*i =0,071175164-0,522218224i=1/6*sqrt(10)*cis(277,76°)
v1=vc^(1/3)=(1/8*sqrt(5)-5/24)+(1/24*sqrt(15)+5/24*sqrt(3))*i =0,071175164+0,522218224i=1/6*sqrt(10)*cis(82,24°)
v2=v1*cis(120°)=(-1/8*sqrt(5)-5/24)+(sqrt(5/32-5/96*sqrt(5)))*i =-0,487841831-0,199469612i=1/6*sqrt(10)*cis(202,24°)
v3=v1*cis(240°)=5/12-1/12*sqrt(15)i=0,416666667-0,322748612i =1/6*sqrt(10)*cis(322,24°)
Suche zu einander passende u und v so mit u*v=-p/3!
Die folgenden 4 Werte sind gleich:
-p/3=5/18
u1*v3=5/18
u2*v2=5/18
u3*v1=5/18
z1=u1+v3=5/6
z2=u2+v2=-1/4*sqrt(5)-5/12
z3=u3+v1=1/4*sqrt(5)-5/12
Resubstitution
y1=z1-b1/3=1
y2=z2-b1/3=-1/4-1/4*sqrt(5)
y3=z3-b1/3=1/4*sqrt(5)-1/4
Eine Lösung y genügt
y=y1=1
s=(1/4*(b/a)^2+2*y-c/a)^(1/2)=1/2*sqrt(5)=1,118033989
t=(b/a*y-d/a)/(2*s)=0
Falls s=0 t=(y^2-e/a)^(1/2)
Zu Lösen bleibt
x^2+r1*x+w1=0 und x^2+r2x+w2=0
r1=b/(2*a)+s=1/2+1/2*sqrt(5)=1,618033989
w1=y+t=1
r2=b/(2*a)-s=-1/2*sqrt(5)+1/2=-0,618033989
w2=y-t=1
Somit: x4+x3+x2+x+1=(x2+(1/2+1/2*sqrt(5))x+1)*(x2+(1/2-1/2*sqrt(5))x+1)
x1=-r1/2+((r1/2)^2-w1)^(1/2) =(-1/4-1/4*sqrt(5))+(sqrt(5/8-1/8*sqrt(5)))*i =-0,809016994+0,587785252i=cis(144°)
x2=-r1/2-((r1/2)^2-w1)^(1/2) =(-1/4-1/4*sqrt(5))+(sqrt(5/8-1/8*sqrt(5)))*i =-0,809016994-0,587785252i=cis(216°)
x3=-r2/2+((r2/2)^2-w2)^(1/2) =(1/4*sqrt(5)-1/4)+(sqrt(1/8*sqrt(5)+5/8))*i =0,309016994+0,951056516i=cis(72°)
x4=-r2/2-((r2/2)^2-w2)^(1/2) =(1/4*sqrt(5)-1/4)+(sqrt(1/8*sqrt(5)+5/8))*i =0,309016994-0,951056516i=cis(288°)
Vier komplexe Lösungen:
x3=cis(72°)
x1=cis(144°)
x2=cis(216°)
x4=cis(288°)
Bemerkung: Da x4+x3+x2+x+1=(x5-1):(x-1) ist, sind
die erhaltenen Nullstellen die Einheitswurzeln ohne die 1 von x5=1 .
x3=cis(72°)
x1=cis(144°)
x2=cis(216°)
x4=cis(288°)
b) x4-x3+x2-x+1=0
a=1
b=-1
c=1
d=-1
e=1
Die kub. Gl. y^3+b1y^2+c1y+d1=0 ...
b1=-c/(2*a)=-1/2
c1=1/4*(b*d/a-4*e)/a=-3/4
d1=1/8*(4*c*e-b*b*e/a-d*d)/(a*a)=1/4
... wird auf die red. kub. Gl.
z^3+p*z+q=0 zurückgeführt.
Subst. x=z-b/(3*a)
p=c1-b1^2/3=-5/6
q=2/27*b1^3-1/3*b1*c1+d1=25/216
Lösung von z^3 + pz + q = 0
nach Cardano
dd=(q/2)^2+(p/3)^3=-125/6912
Bedeutung: uc=u^3 vc=v^3
uc=-q/2+dd^(1/2)=(-25/432)+5/144*sqrt(15)i =-0,05787037+0,134478588i =5/108*sqrt(10)*cis(113,28°)
vc=-q/2-dd^(1/2)=(-25/432)-5/144*sqrt(15)i =-0,05787037-0,134478588i =5/108*sqrt(10)*cis(246,72°)
u1=uc^(1/3)=5/12+1/12*sqrt(15)i =0,416666667+0,322748612i=1/6*sqrt(10)*cis(37,76°)
u2=u1*cis(120°)=(-1/8*sqrt(5)-5/24)+(sqrt(5/32-5/96*sqrt(5)))*i =-0,487841831+0,199469612i =1/6*sqrt(10)*cis(157,76°)
u3=u1*cis(240°)=(1/8*sqrt(5)-5/24)+(1/24*sqrt(15)+5/24*sqrt(3))*i =0,071175164-0,522218224i =1/6*sqrt(10)*cis(277,76°)
v1=vc^(1/3)=(1/8*sqrt(5)-5/24)+(1/24*sqrt(15)+5/24*sqrt(3))*i =0,071175164+0,522218224i =1/6*sqrt(10)*cis(82,24°)
v2=v1*cis(120°)=(-1/8*sqrt(5)-5/24)+(sqrt(5/32-5/96*sqrt(5)))*i =-0,487841831-0,199469612i =1/6*sqrt(10)*cis(202,24°)
v3=v1*cis(240°)=5/12-1/12*sqrt(15)i =0,416666667-0,322748612i =1/6*sqrt(10)*cis(322,24°)
Suche zu einander passende u und v so mit u*v=-p/3!
Doe folgenden 4 Werte müssen gleich sein:
-p/3=5/18
u1*v3=5/18
u2*v2=5/18
u3*v1=5/18
z1=u1+v3=5/6=0,833333333
z2=u2+v2=-1/4*sqrt(5)-5/12=-0,975683661
z3=u3+v1=1/4*sqrt(5)-5/12=0,142350328
Resubstitution
y1=z1-b1/3=1
y2=z2-b1/3=-1/4-1/4*sqrt(5)=-0,809016994
y3=z3-b1/3=1/4*sqrt(5)-1/4=0,309016994
Eine Lösung y genügt
y=y1=1
s=(1/4*(b/a)^2+2*y-c/a)^(1/2)=1/2*sqrt(5)=1,118033989
t=(b/a*y-d/a)/(2*s)=0
Falls s=0 t=(y^2-e/a)^(1/2)
Zu Lösen bleibt
x^2+r1*x+w1=0 und x^2+r2x+w2=0
r1=b/(2*a)+s=1/2*sqrt(5)-1/2=0,618033989
w1=y+t=1
r2=b/(2*a)-s=-1/2-1/2*sqrt(5)=-1,618033989
w2=y-t=1
x1=-r1/2+((r1/2)^2-w1)^(1/2)=(-1/4*sqrt(5)+1/4)+(sqrt(1/8*sqrt(5)+5/8))*i =-0,309016994+0,951056516i=cis(108°)
x2=-r1/2-((r1/2)^2-w1)^(1/2)=(-1/4*sqrt(5)+1/4)+(sqrt(1/8*sqrt(5)+5/8))*i =-0,309016994-0,951056516i=cis(252°)
x3=-r2/2+((r2/2)^2-w2)^(1/2)=(1/4+1/4*sqrt(5))+(sqrt(5/8-1/8*sqrt(5)))*i =0,809016994+0,587785252i=cis(36°)
x4=-r2/2-((r2/2)^2-w2)^(1/2)=(1/4+1/4*sqrt(5))+(sqrt(5/8-1/8*sqrt(5)))*i =0,809016994-0,587785252i=cis(324°)
Vier komplexe Lösungen:
x1=(-1/4*sqrt(5)+1/4)+(sqrt(1/8*sqrt(5)+5/8))*i
x2=(-1/4*sqrt(5)+1/4)+(sqrt(1/8*sqrt(5)+5/8))*i
x3=( 1/4+1/4*sqrt(5))+(sqrt(5/8-1/8*sqrt(5)))*i
x4=( 1/4+1/4*sqrt(5))+(sqrt(5/8-1/8*sqrt(5)))*i
x1=(-1/4*sqrt(5)+1/4)+(sqrt(1/8*sqrt(5)+5/8))*i
x2=(-1/4*sqrt(5)+1/4)+(sqrt(1/8*sqrt(5)+5/8))*i
x3=( 1/4+1/4*sqrt(5))+(sqrt(5/8-1/8*sqrt(5)))*i
x4=( 1/4+1/4*sqrt(5))+(sqrt(5/8-1/8*sqrt(5)))*i
c) 4x4+2x3+x2+2x+4=0
a=4
b=2
c=1
d=2
e=4
Die kub. Gl. y^3+b1y^2+c1y+d1=0 ...
b1=-c/(2*a)=-1/8
c1=1/4*(b*d/a-4*e)/a=-15/16
d1=1/8*(4*c*e-b*b*e/a-d*d)/(a*a)=1/16
... wird auf die red. kub. Gl.
z^3+p*z+q=0 zurückgeführt.
Subst. x=z-b/(3*a)
p=c1-b1^2/3=-181/192
q=2/27*b1^3-1/3*b1*c1+d1=161/6912
Lösung von z^3 + pz + q = 0 nach Cardano
dd=(q/2)^2+(p/3)^3=-54665/1769472
Bedeutung: uc=u^3 vc=v^3
uc=-q/2+dd^(1/2)=(-161/13824)+29/2304*sqrt(195)i =-0,011646412+0,175765174i =0,176150604*cis(93,79°)
vc=-q/2-dd^(1/2)=(-161/13824)-29/2304*sqrt(195)i =-0,011646412-0,175765174i =0,176150604*cis(266,21°)
u1=uc^(1/3)=23/48+1/48*sqrt(195)i =0,479166667+0,290921668i =1/24*sqrt(181)*cis(31,26°)
u2=u1*cis(120°)=-0,491528888+0,269509672i =1/24*sqrt(181)*cis(151,26°)
u3=u1*cis(240°)=0,012362221-0,56043134i =1/24*sqrt(181)*cis(271,26°)
v1=vc^(1/3)=0,012362221+0,56043134i =1/24*sqrt(181)*cis(88,74°)
v2=v1*cis(120°)=-0,491528888-0,269509672i =1/24*sqrt(181)*cis(208,74°)
v3=v1*cis(240°)=23/48-1/48*sqrt(195)i =0,479166667-0,290921668i =1/24*sqrt(181)*cis(328,74°)
Suche zu einander passende u und v so mit u*v=-p/3!
Die folgenden 4 Werte sind gleich:
-p/3=181/576
u1*v3=181/576
u2*v2=181/576
u3*v1=181/576
z1=u1+v3=23/24
z2=u2+v2=-0,983057776=-1/16*sqrt(65)-23/48
z3=u3+v1=0,024724443=1/16*sqrt(65)-23/48
Resubstitution
y1=z1-b1/3=1
y2=z2-b1/3=-0,941391109=-7/16-1/16*sqrt(65)
y3=z3-b1/3=0,066391109=1/16*sqrt(65)-7/16
Eine Lösung y genügt
y=y1=1
s=(1/4*(b/a)^2+2*y-c/a)^(1/2)=1/4*sqrt(29)=1,346291202
t=(b/a*y-d/a)/(2*s)=0
Falls s=0 t=(y^2-e/a)^(1/2)
Zu Lösen bleibt
x^2+r1*x+w1=0 und x^2+r2x+w2=0
r1=b/(2*a)+s=1/4+1/4*sqrt(29)=1,596291202
w1=y+t=1
r2=b/(2*a)-s=-1/4*sqrt(29)+1/4=-1,096291202
w2=y-t=1
Somit: 4x4+2x3+x2+2x+4 = (x2-(1/4+1/4*sqrt(29)x+1)*(x2-(1/4-1/4*sqrt(29)x+1)
x1=-r1/2+((r1/2)^2-w1)^(1/2) =(-1/8-1/8*sqrt(29))+(sqrt(17/32-1/32*sqrt(29)))*i =-0,798145601+0,602464605i=cis(142,95°)
x2=-r1/2-((r1/2)^2-w1)^(1/2) =(-1/8-1/8*sqrt(29))+(sqrt(17/32-1/32*sqrt(29)))*i =-0,798145601-0,602464605i=cis(217,05°)
x3=-r2/2+((r2/2)^2-w2)^(1/2) =(1/8*sqrt(29)-1/8)+(sqrt(1/32*sqrt(29)+17/32))*i =0,548145601+0,836382927i=cis(56,76°)
x4=-r2/2-((r2/2)^2-w2)^(1/2) =(1/8*sqrt(29)-1/8)+(sqrt(1/32*sqrt(29)+17/32))*i =0,548145601-0,836382927i=cis(303,24°)
Vier komplexe Lösungen:
x1=(-1/8-1/8*sqrt(29))+(sqrt(17/32-1/32*sqrt(29)))*i
x2=(-1/8-1/8*sqrt(29))+(sqrt(17/32-1/32*sqrt(29)))*i
x3=(1/8*sqrt(29)-1/8)+(sqrt(1/32*sqrt(29)+17/32))*i
x4=(1/8*sqrt(29)-1/8)+(sqrt(1/32*sqrt(29)+17/32))*i
x1=(-1/8-1/8*sqrt(29))+(sqrt(17/32-1/32*sqrt(29)))*i
x2=(-1/8-1/8*sqrt(29))+(sqrt(17/32-1/32*sqrt(29)))*i
x3=(1/8*sqrt(29)-1/8)+(sqrt(1/32*sqrt(29)+17/32))*i
x4=(1/8*sqrt(29)-1/8)+(sqrt(1/32*sqrt(29)+17/32))*i