Die Homepage von Joachim Mohr
Quelle Deutsche digitale Bibliotek
Die Tanaka-Orgel (pdf)
Das Tanaka-Parallelogramm
Studien im Gebiete der reinen Stimmung
von Shoé Tanaka (1890) 90 Seiten - Excerpt
Die im folgenden niedergelegten Untersuchungen gliedern sich in vier Abschnitte:
I Über das reine Tonsystem.
II Über ein reigestimmtes Harmonium.
III Die ältere harmonische Kunst im Lichte der reinen Stimmung.
IV Zur Geschichte der Temperierten und reingestimmten Tasteninstrumente in früheren Jahrhunderten.
S2. Die pythagoreische Quintenreihe (reine Quinten mit dem Frequenzverhältnis 3/2), die auf eine Oktave reduziert sind
Aufwärts: c g d a e h fis cis gis dis ais eis his fisis cisis ...
Abwärts: c f b es as des ges ces fes bb eses ases deses ...
Nehmen wir nun die reingestimmte Obergroßterz (Frequenzverhältnis 5/4), so ist dies nicht der schon oben aufgeführte Ton e, sondern ein anderer, der ein wenig tiefer liegt. Wir unterscheiden diesen neuen Ton von jenem durch ein "Tiefkomma" [Bei Tanaka durch einen Unterstrich]. So heißt der Durdreiklang auf c:
c-,e-g
S.3 Die Obergroßterz irgend eines Tones ist um ein (syntonisches) Komma (Frequenzverhältnis 81/80) tiefer als dessen 4. Quinte.S4 Die kleine Terz von irgend einem Tone ist ein Komma höher als dessen dritte Quarte. Der Ton es ist die dritte Unterquinte von c und 'es die kleine Terz von c. Der Ton 'b, die Quinte von 'es und zugleich die kleine Terz von g, ist ein Komma höher als b, die zweite Unterquinte von c usw.
s.5ff Darstellung des Tonnetzes
S8 Schismatische Verwechslung
Töne - obgleich numerisch verschiendenartig - sich dennoch einander so nahe kommen, dass unser Gehör sie nicht mehr von einander zu unterscheiden vermag. In der Tat müssen einige Töne innerhalb der Grenzen des Ununterscheidbaren zusammenfallen....
,h und ces unterscheiden sich um das "Schisma" mit dem Frequenzverhätnis
5/4•1/2•(9/8/)4=32805/32768 ≙ 1,9537 Cent [in heutiger Schreibweise].
Fußnote: Artusi berechnete die Größe des Schismas auf S.22 seines Buches "Imperfettioni della musica moderna", Venedig 1960.
S.9 Dieses Schisma verursacht erst in der Höhe des zweigestrichenen a ungefähr eine Schwebung in einer Sekunde, und die durch dieses äußerst kleine intervall verursachende Unreinheit der Harmonie wird schwerlich zu empfinden sein.
Also:,h=ces ebenso ,,ais=,b / fis='ges
,fis=ges /,,eis=,f / cis='des
,cis=des / ,,his=,c / gis='as
,gis=as / ,,fisis=,g / dis='es
,dis=es / ,,cisis =d / ais='b
...
Kleismatische Verwechslung
Ferner wollen wir das Intervall zwischen einem Tone aus einer in der Tabelle diagonal verlaufenden Reihe der Terzschritte und den hinsichtlich der Tonhöhe ihm am nächsten liegenden Ton aus der benachbartenReihe abmessen.
Vergleichen wir beispielsweise '''fes und ,,,eis.
Von '''fes aus gelangt man auf der Tabelle zu ,,,ais, der oberen Quarte von ,,,eis, durch folgende Kleinterzschritte:
'''fes-''des-'b-g-,e-,,cis-,,,ais.
Indem man hier durch Multiplikation mit 4 die Töne zu derselben Oktave bring, erhält man:
,,,ais:'''fes=4•(5/6)6
aber ,,,eis:,,,ais=3:4
mithin
,,,eis:'''fes=4•(5/6)6•3/4=15625/15552 ≙ 8,107 Cent [in heutiger Schreibweise].
Kleisma = 6(große Terzen)+1Oktave-5Quinten ≈ 8,107 Cent.
Fußnote: Rameau berechnete das Intervall des Kleisma in der Tabelle auf S.26 seines Buches "Nouveau Sysème des Musique théorique, Paris 1726.
S10 Dieses letzte Intervall, welches ich "Kleisma" (grichisch: "Verschluss")nennen will, bildet ebenfalls einen kleinen Unterschied, der sich in höheren Lagen nur bei gespannter Aufmersamkeit wahrnehmen läßt. Man kann deshalb in Modulationsfällen mit genügender Reinheit setzen:
'''ges=,,,fisis / ebenso ''b=,,,,aissis / u.s.f
'''ces=,,,his / ''es=,,,,disis
'''fes=,,,eis / ''as =,,,,gisis
'''b=,,,ais / ''des=,,,,cisis
'''eses=,,,dis / ''ges=,,,,fisis
...
Durch diese Vertauschung, die man analog "kleismatische Verwechslung" nennen kann, werden die äußeren Terztöne miteinander verbunden. Dieselbe findet im Allgemeinen statt, wenn man in der Tabelle von der unteren Quinte eines beliebigen Tones sechs Kleinterzschritte aufwärts macht; hierdurch wird theoretisch eine Erniedrigung um ein Kleisma eintreten.
System der 53 reinen Intervalle
Durch Anwendung der schismatischen und kleismatischen Verwechslung wird die Anzahl der selbständigen Töne auf die folgenden 53 Stufen reduziert
(Die Zahlen geben den Ort der Töne in der Mercator-Tabelle an:
Tabelle II
,,,fis ,,,cis ,,,gis ,,,dis ,,,ais ,,,eis ,,,his ,,,fisis
24 2 33 11 42 20 51 29
/ \ / \ / \ / \ / \ / \ / \ / \
/ \ / \ / \ / \ / \ / \ / \ / \
/ \ / \ / \ / \ / \ / \ / \ / \
,,d ,,a ,,e ,,h ,,fis ,,cis ,,gis ,,dis ,,ais
7 38 16 47 25 3 34 12 43
\ / \ / \ / \ / \ / \ / \ / \ / \
\ / \ / \ / \ / \ / \ / \ / \ / \
\ / \ / \ / \ / \ / \ / \ / \ / \
,f ,c ,g ,d ,a ,e ,h ,fis ,cis
21 52 30 8 39 17 48 26 4
\ / \ / \ / \ / \ / \ / \ / \ / \
\ / \ / \ / \ / \ / \ / \ / \ / \
\ / \ / \ / \ / \ / \ / \ / \ / \
as es b f c g d a e
35 13 44 22 0 31 9 40 18
\ / \ / \ / \ / \ / \ / \ / \ / \
\ / \ / \ / \ / \ / \ / \ / \ / \
\ / \ / \ / \ / \ / \ / \ / \ / \
'ces 'ges 'des 'as 'es 'b 'f 'c 'g
49 27 5 36 14 45 23 1 32
\ / \ / \ / \ / \ / \ / \ / \ / \
\ / \ / \ / \ / \ / \ / \ / \ / \
\ / \ / \ / \ / \ / \ / \ / \ / \
''eses ''bb ''fes ''ces ''ges ''des ''as ''es ''b
10 41 19 50 28 6 37 15 46
In der 53er Mercatortabelle:
0 1 2 3 4 5 6 7 8 9
c 'c ,,,cis,,cis,cis 'des ''des,,d ,d d
10 11 12 13 14 15 16 17 18 19
''eses ,,,dis,,dis es 'es ''es ,,e ,e e ''fes
20 21 22 23 24 25 26 27 28 29
,,,eis ,f f 'f,,,fis ,,fis ,fis 'ges''ges,,,fisis
30 31 32 33 34 35 36 37 38 39
,g g 'g ,,,gis ,,gis as 'as ''as ,,a ,a
40 41 42 43 44 45 46 47 48 49
a ''bb ,,,ais,,ais b 'b ''b ,,h ,h 'ces (bb=heses)
50 51 52
''ces ,,,his ,c
S.12 1) Wenn man eine der schrägen Seiten des Parallelogramms von links nach rechts überschreitet, so wird jeder Ton um ein Schisma höher, und umgekehrt.
Beispiel: Rechts oben käme nach ,,,fisis der Ton ,,,cisis = ,,d + Schisma
2) Wenn man eine der waagrechten Seiten des Parallelogramms von oben nach unten überschreitet, so tritt eine Erniedrigung der Höhe für entsprechende Töne um ein Kleisma ein, und umgekehrt.
Beispiel: Links oben käme über ,,,fis (nach links) ,,,,dis = ''eses + Kleisma
...
Wenn man sich damit begnügt, in den äußersten Modulationsfällen, d.h. wenn die Töne außerhalb der Grenzen eines Parallelogramms zur Anwendung gebracht werden, die beiden Verwechslungen wirklich eintreten zu lassen, so gestattet die 53stufige Leiter absolute Freiheit der Modulation nach allen Richtungen.
Bemerkung von J.M.: Wenn man allerdings 5 Zeilen nach oben das Tanaka-Parallelogramm fortsetzt, dann überschreitet man deutlich den Fehler über das Kleisma. Siehe hier
x=,,,,,,,,,,,disisisisisis (8 Kommata und 6 mal "is", also gleichstig der Ton gis)
Entweder x=''ges+18 Cent oder x=,,,fisis-11 Cent.
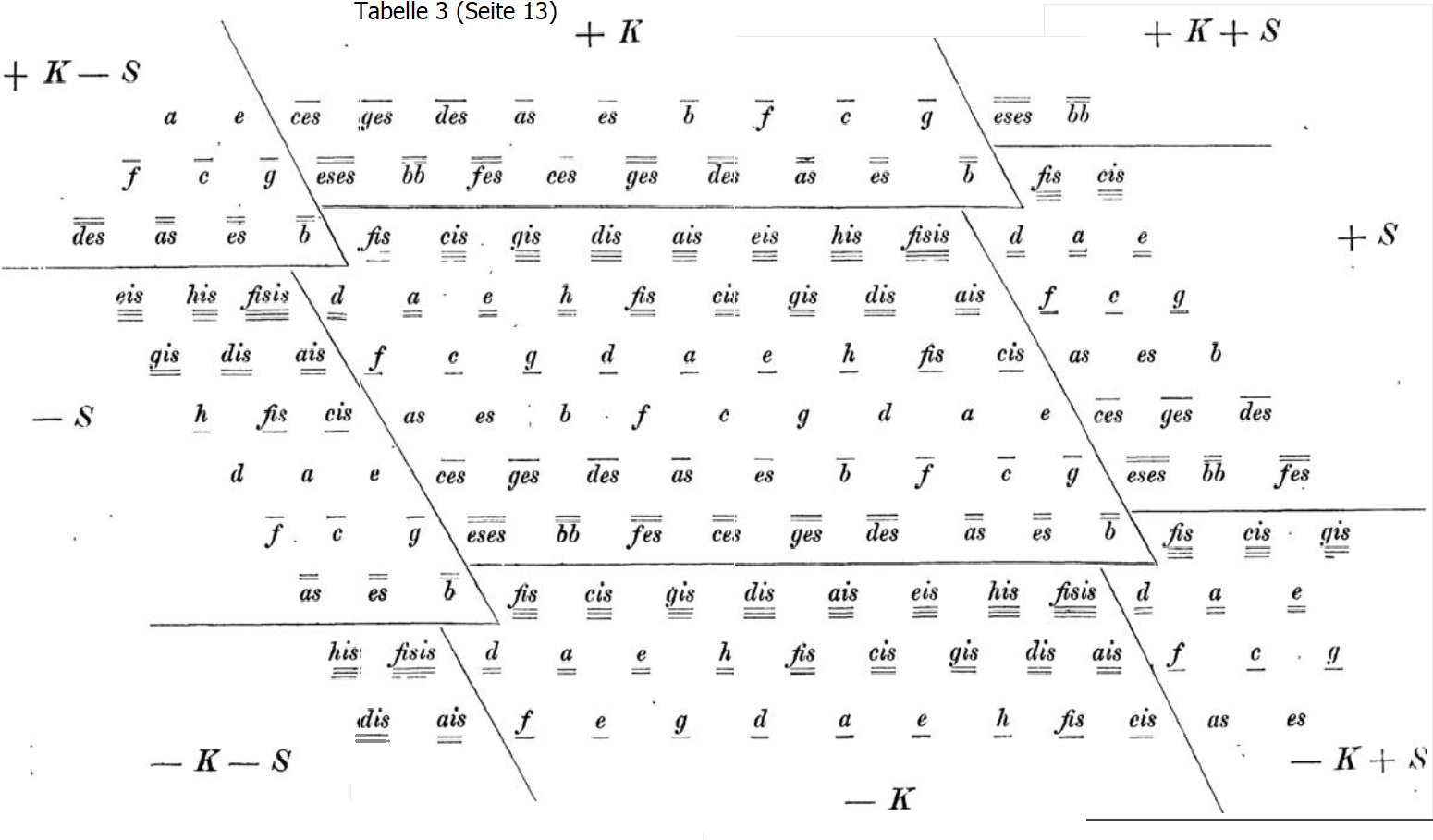
Bilderklärung: K: Kleismaische Verwechslung (± 8 Cent) S: Schismatische Verwechslung (± 2 Cent)
S.17
Durch wieviel Quintenschritte ist die Oktave möglichst nahe zu erreichen?
Die erste Annäherung findet nach 12 solcher Schritte statt, wobei die 7. Oktave um ein kleines Intervall, pythagoreisches Komma genannt, überschritten wird. Indem man die Quinten um ein Zwölftel dieses Kommas verkleinerte, entstand die moderne 12-stufige gleichschwebende Temperatur. Die nächste Annäherung erfolgt bei der 31. Oktave und der 53. Quinte. Wenn man nun die an sich sehr kleine Differenz [3,6 Cent] in 53 gleiche Teile teilt, und diese auf die 53 Quinten verteilt, so sind die Unreinheiten nicht bemerkbar.
Bei der so erlangten Temperatur wurde die Terz außer Acht gelassen, und wenn die 17. Stufe der so geteilten Oktave zufälligerweise der großen Terz sehr nahe kommt, so war dies nicht vorausgesehen worden. [Die 17. Stufe ist um 1,4 Cent im Vergleich zur großen Terz zu klein.]
S.18 [betrifft die Teilung der Oktave in 53 Teile]..., so brauchen wir weder die schismatische noch die kleismatischen Verwechslungen vornehmen.
S.19 [Zur gleichstufigen Stimmung] Bei dem Klavier sind die Verhältnisse besonders günstig, da die Töne sich nach dem Anschlagen gleich abschwächen, und somit die Schwebungen der unreinen Akkorde weniger empfunden werden. Dagegen tritt bei Pfeifen- und Zungenwerken die Missstimmung wegen der anhaltenden Stärke der Töne bedeutend hervor. Die Quinten sind hier zwar befriedigend rein gestimmt, aber es sind die etwas zu hoch genommenen Terzen, welche den Wohlklang stören.
II Über ein reingestimmtes Harmonium.
[Hier beschreibt Tanaka ein kompliziert aufgebautes Harmonium mit Zwischentasten und Umschalttasten]
III Die ältere harmonische Kunst im Lichte der reinen Stimmung.
S. 44ff Gegen Ende des 15. und am Anfang des 16. Jahrhunderts begegnen wir in Italien jener herrlichen Renaissance-Zeit, welche sich zunächst in den bildenden Künsten offenbarten ... Die Berechnungen der Proportionen, die Theileung der Intervalle wurden nochmals aufgenommen.
...
Ein Spanier, namens Bartholomeus Ramis war der erste, der in seiner Schrift "De Musica tractatus", Bolognia 1482 auf die Nothwendigkeit einer Temperatur aufmarksam machte. Er scheint zur Ansicht gekommen zu sein, dass die großen und kleinen Terzen als Konsonanten die von Didymus und Ptolemaus gefundenen Proportionen 5/4 und 6/5 haben müssen., und dass , wenn das Komma eben die Abweichung dieser von denen des Pythagoras, in der Praxis nicht außer Acht gelassen werden konnte, dasselbe durch eine neue Vertheilung der Intervalle der Tonleiter zu beseitigen sei. Hiermit verkündete er den fruchtbaren Gedanken einer endlichen Aufhebung jenes seit mehr als zwei Jahrhunderten chronisch gewordenen Übels im Tonsystem...
Doch verdanken wir die vollständige Aufklärung über diese Frage der klaren Einsicht und tief wissenschaftlicher Methodik des Gioseffo Zarlino (1517-1599). In seinem epochemachenden Wek "Institutioni harmoniches", zuerst in Venedig 1557 erschienen, prüft er aufs gründlichste die auf arithmetischen Teilungen der Proportionen begründeten Musiksysteme der griechischen Gelehrten ...
die pythagoreische Terz mit der Proportion 81/64 als eine entschiedene Dissonanz, findet dagegen die Terzen nach ptolemäischer Bestimmung das Gehör sehr angenehm berührend und endlich empffielt er folgende natürliche oder syntonische Diatonik von Ptolemäus
c 9/8 d 10/9 ,e 16/15 f 9/8 g 10/9 ,a 10/9 ,h 16/15 c
als das einzig natürliche Tonsystem.
Jedoch findet er, dass die richtige Quarte der sechsten Stuf ,a nicht der Ton d, sondern ane anderer, ein Komma (81/80) tieferen Ton ,d sei, und macht Vorschläge zur Beseitigung dieses störenden Elementes durch den zum ersten Male konsequent durchgeführten Plan zur Temperierung der Intervalle...
S.50 ... werde ich nunmehr folgendes Beispiel aus dem Fux'schem "Gradus ad Parnassum" von Johann Joseph Fux (das lateinische Original wurde 1725 in Wien gedruckt), welches als das beste Lehrbuch über den Kontrapunkt galt, betrachten:
| Rechts die Akkorde in Eulerschreibweise
In den meisten Akkorden kommt ,d vor, bei G-Dur Akkorden jedoch d, ein Komma höher. 
|
Einfügung von J.M.
,d ,a ,d f
,d f f ,a
c g ,e c
g d ,h
,e g g ,h
,d ,a f ,d
f ,a ,a c
c c g ,e
,d ,a ,a
,a ,a ,e ,,cis
,d ,a ,d ,d
,d f ,a ,d
,d f ,a f
c g c ,e
g ,h d
,e g ,h g
,d ,a ,d f
f ,a c ,a
c c ,e g
,d ,a ,d f
,a ,a ,,cis ,e
,d ,a ,d
,d ,a f
,d f ,a ,d
,a ,e ,a c
b ,d f ,d
g g 'b d
,d f ,a f
,a ,a c ,e
c g c ,e
,d f ,a ,d
,a ,e ,a ,,cis
,d ,a ,d
,d ,d f ,a
f ,d f ,a
,e ,g ,g ,,cis
,d ,a f ,d
,g b ,d b
f c f ,a
,a c ,e ,a
,g ,d ,g ,,h
,d f ,a ,d
,e ,g ,g ,,cis
,d ,a ,,fis ,d
|
