Vom Winkelsummensatz über den Satz des Thales
zum Zentriwinkelsatz

Erläuterung: siehe unten.

---

Der Winkelsummenstz

Die Summe der Winkel im Dreieck ist 180° (gleich dem gestreckten Winkel)

α+β+γ=180°

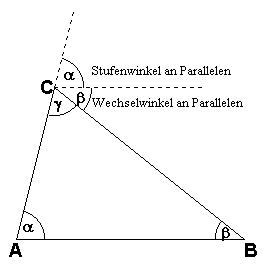
Beweis: Mit Stufenwinkel α und Wechselwinkel β an der Parallelen von AB durch C sieht man: γ+β+α=gestreckter Winkel=180°. ∎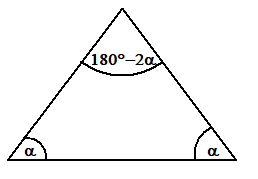

---

Wir benötigen im Folgenden für das gleichschenklige Dreieck (α=β):

γ=180°-2α

Zum Beispiel α=53° ⇒ γ=180°-106°= 74°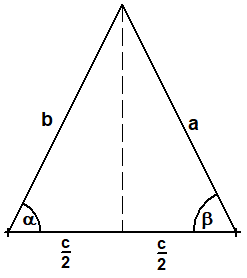

---

Der Basiswinkelsatz

a=b ⇒ α = β

Satz:In einem gleichschenkligen Dreieck sind die Basiswinkel gleich, d.h. a=b ⇒ α = β
Beweis: Halbiert mn die Basis c, so erhält man zwei Dreiecke mit gleich großen entsprechenden Seiten. Nach dem Kongruenzsatz SSS sind dann entsprechende Winkel sind dann gleich. Also α = β ∎

Die Umkehrung gilt auch:

α = β ⇒ a=b

Beweis: Nach dem Kongruenzsatz SWS ∎

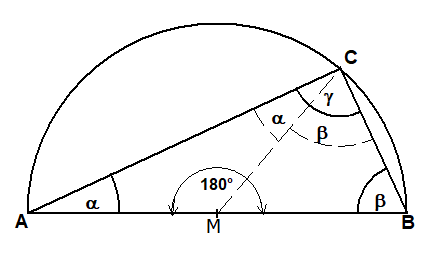
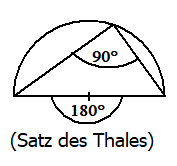
Satz des Thales

Der Winkel im Halbkeis ist ein rechter Winkel.

γ=90°

Beweis: Im gleichschenkligen Dreieck sind die Basiswinkel bei A und C gleich α und im gleichschenkligen Dreieck BMC sind die Basiswinkel bei B und C gleich β.
Für die Winkelsumme im Deieck ABC gilt dann
α+β+γ=α+β+α+β=2(α+β)=180° also γ=α+β=90°> ∎

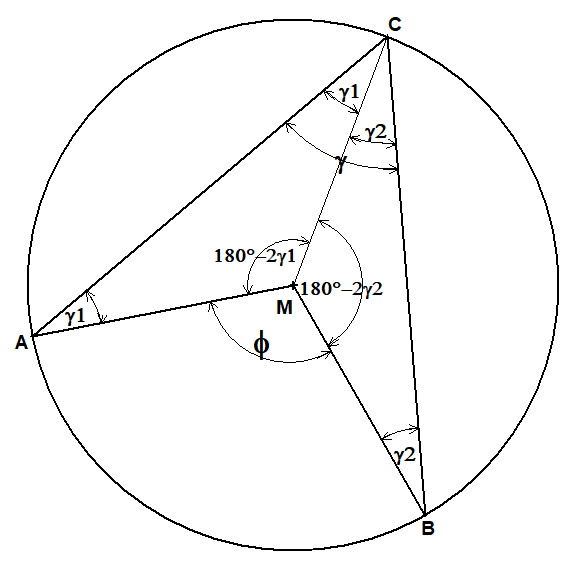
Zentriwinkelsatz

Satz: Der Mittelpunktswinkel (Zentriwinkel) φ=∡AMB ist doppelt so groß wie der zugehörige Umfangswinkel (Peripheriewinkel) γ=∡ACB.

φ=2γ

Egal wo C auf der Kreislinie liegt: Der Umfangswinkel γ ist überall gleich groß.

Beweis:
Im gleichschnekligen Dreieck AMC sind die zwei Basiswinkel γ₁ bei A und C gleich.
Der Dritte Winkel ∡AMC ist dann nach dem Winkelsummensatz 180°- 2γ₁.

Im gleichschnekligen Dreieck BMC sind die zwei Basiswinkel γ₂ bei B und C gleich.
Der Dritte Winkel ∡BMC ist dann nach dem Winkelsummensatz 180°- 2γ₁.

Der Vollwinkel bei M mit 360° ist die Summe von drei Winkel. Also:

(180°-2γ₁)+(180°-2γ₂)+φ=360°
⇒ -2γ₁-2γ₂+φ=0
⇒ φ=2(γ₁+γ₂)=2γ ∎

Die Punkte A, B und C können auch auf einem Halbkreis liegen (siehe Zeichnung). Auch hier gilt
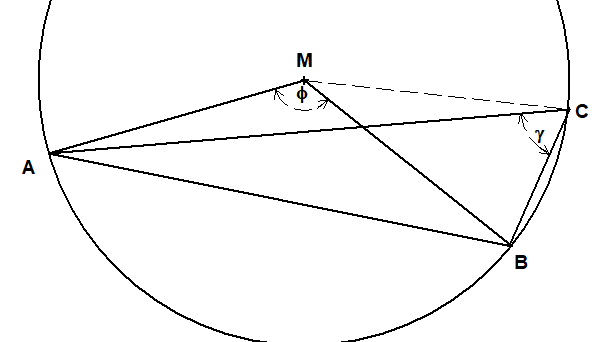
φ = 2γ .
Sei γ₁=∡CAM. Das bedeutet: Der Winkel ist bei A und die Strecke CA wird mathematisch positiv um den Winkel γ₁ gedeht, so dass die gedrehte Strecke auf AM liegt.

Seien also im gleichschenkligen Dreieck ACM:
γ₁=∡CAM=∡MCA
und im gleichschenkligen Dreieck BMC:
γ₁+γ=∡BCM=∡MBC

Dann ist im gleischenkligen Dreieck ABM der dritte Winkel
∡AMC=180°-2γ₁
und im gleichschenkligen Dreieck MBC
∡BMC=180°-2γ₁-2γ.
Die Differenz ist φ. Also φ=180°-2γ₁-(180°-2γ₁-2γ)=2γ ∎

---

---

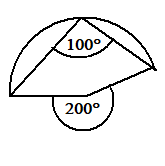
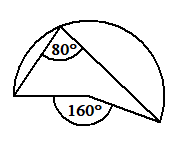
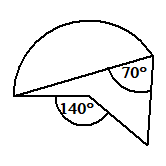
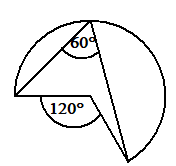
Der Umfangswinkel oben und unten

Hier: γ_o=71,6°. Zugehöriger Mittelpunktswinkel φ_o=143,2°
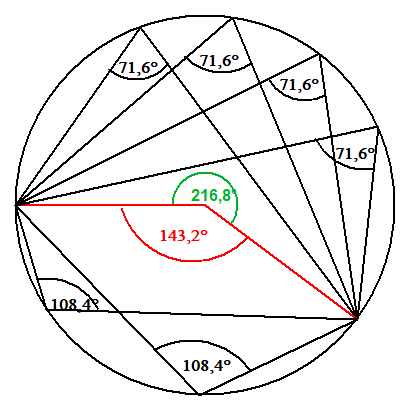
γ_u=108,4°. Zugehöriger Mittelpunktswinkel φ_u=216,8°

Satz:     φ    =2γ        φ     =2γ
           o      o        u       u

Beispiel 143,2°=2·71,6°   216,8°=2·108,4°


Satz:     φ      + φ      = 360°
           o        u

Beispiel: 143,2° + 216,8° = 360°


Satz:    γ    + γ      = 180°
          o      u

Beispiel: 71,6°+108,4° = 180°