Die Homepage von Joachim Mohr
Aus der Vektorrechnung
- Lektionen der Vektorrechnung in Aufgaben
- Der Schwerpunktsatz
- Einführung in das Skalarprodukt
- Abstand Punkt - Ebene (Hesse-Form)
- Formel für Abstand windschiefer Geraden
- Koeffizientenvergleich
Der Schwerpunktsatz
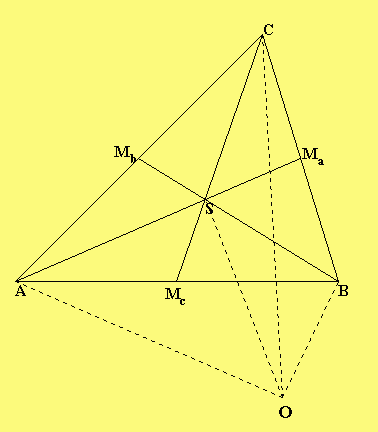
Kleinbuchstaben mit Pfeil bezeichnen Ortsvektoren: -> ——> -> ——> -> ——> -> ——> a = OA, b = OB, c = OC ,s = OS u.s.w.
Jetzt wird gerechnet:
-> -> 1——> -> 1 -> -> 1-> 1->
m = b + -BC = b + -(c - b) = -b + -c
a 2 2 2 2
-> 1-> 1-> -> 1-> 1->
Analog m = -a + -c und m = -a + -b.
b 2 2 c 2 2
("Mitte von zwei Punkten = Mittelwert").
S sei der Punkt auf AM , der von A den
a
2——
Abstand -AM hat:
3 a
-> -> 2 ——> 2 -> ->
s = a + - AM = a + -(m - a)
3 a 3 a
-> -> ->
-> 2 1-> 1-> -> a + b + c
=a + - (-b + -c - a) = —————————
3 2 2 3
Genau denselben Punkt erhält man, wenn man
auf BM bzw. CM den Punkt sucht, der von
b c
2—— 2——
B bzw. C den Abstand -BM bzw. -CM hat.
3 b 3 c
S liegt also auf allen drei Seitenhalbierenden und
heißt Schwerpunkt. Somit ist bewiesen:Der Schwerpunkt S teilt die Seitenhalbierenden (Schwerelinien) im Verhältnis 2:1. Und: Für den Schwerpunkt S gilt:
|
Beispiel zur Anwendnung des Schwerpunktsatzes:
——> ——> Nachtrag: Ist AS = 2·SM , so "teilt S die Strecke AM im Verhältnis 2:1". a a ——> 2 ——> Dann gilt AS = -·AM ! AS sind 2 Teile, SM ist 1 Teil, zusammen also 3 Teile. 3 a a
Der Schwerpunkt des Dreiecks A(1|3|7)B(6|2|5)C(2|1|0) ist
1 + 6 + 2 3 + 2 + 1 7 + 5 + 0
S(—————————|—————————|—————————), also S(3|2|4)
3 3 3
Ein anderer Beweis, der die Kenntnis vom Teilverhältnis 2:1 nicht verwendet, findet sich als Beispiel zum Koeffizientenvergleich.
Hier der Beweis etwas abgewandelt:
Damit ist gezeigt, dass der Schnittpunkt von zwei Seitenhalbierenden diese im Verhältnis 2:1 teilt.
-> -> ——> -> 1-> 1-> -> Bringe die Geraden (AM ): x = a + sAM = a + s(-b + -c - a ) a a 2 2 -> -> ——> -> 1-> 1-> -> (BM ): x = b + tBM = b + t(-a + -c - b ) b b 2 2 -> zum Schnitt. Der Ortsvektor x des Schnittpunktes kann auf zwei Arten dargestellt werden. Also gilt: -> 1-> 1-> -> -> 1-> 1-> -> a + s(-b + -c - a ) = b + t(-a + -c - b ) 2 2 2 2 -> 1 -> 1 -> 1 -> -> 1 -> (1-s)·a + -s·b + -s·c = -t·a + (1 - t)·b + -t·c 2 2 2 2 Jetzt muss ich für s, und t Zahlen finden, so dass die Koeffizienten gleich sind. ("Koeffizientenvergleich"). Ich löse also das lineare Gleichungssystem: 1 1 1 1 1-s = -t -s = 1 - t -s = -t 2 2 2 2 2 2 Lösung s = - und t = - 3 3
