Joachim Mohr   Mathematik Musik Delphi
≡

Zeichnungen mit TTGeo2

Konstruktion mit Zirkel und Lineal

Komplexe Zahlen werden mit Punkten identifiziert.
Allgemein gilt:
Addition und Subtraktion als Vektoraddition und -Subtraktion.
Multiplikation und Kehrwert reeller Zahlen mit Hilfe des Strahlensatzes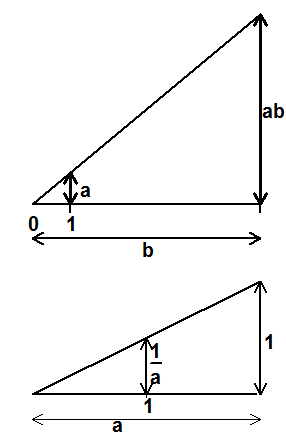 2022strahlensatz
Multiplikation komplexer Zahlen über Polarkoordinaten:
acis(α)·bcis(β)=abcis(α+β) Kehrwert von acis(α)=1/acis(-α) (a,b∈ℝ).
Winkeladdition mit Zirkel und Lineal: Über Kreisabschnitt

Punkte auf der komplexen Zahlenebene, die mit Zirkel und Lineal konstruiert werden können:

Hier komplizierter

Ausgehend von den Punkten 0 und 1 kann konstruiert werden
(a) Der Punkt i (senkrechte auf Geraden durch 0 und 1 und Strecke 01 übertragen auf 0i
(b) Alle Punkte z/n (z∈ℤ, n∈ℕ) auf der Re-Achse und alle Punkte z/ni (z∈ℤ, n∈ℕ) auf der Im-Achse.

Konstruktion zum Beispiel von 5/3

Konstruktion der Parallelen:
(1)Senkrechte durch i zur Geraden durch 3i und 5.
(2)Senkrechte zur Senkrechten durch i.

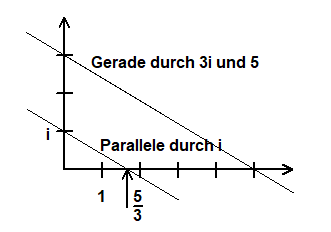
fuenf_drittel
(c) Alle Punkte auf K1=ℚ(i)={a+bi|a,b∈ℚ} (Schnittpunkte von Parallelen zur Re- und Im-Achse).
(d) Außerdem können noch Quadratwurzeln √a (∈ℚ+) konstruiert werden
und man kann dann alle Punkte von K2=ℚ(i,√a) (a∈ℚ+) konstruieren.

Kontruktion von √a (a›0)

Nach dem Höhensatz ergibt sich mit
den Hypothenusenabschnitten 1 und a (a›0)
die Höhe h=√a

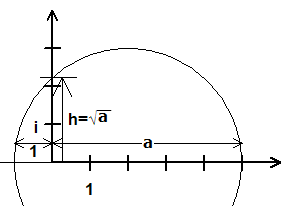
wurzel5
(e) In dieser Körpererweiterung und allen weiteren können Zahlen als Vektoren addiert und subtrahiert werden. Auf diese Weise kann man weitere Wurzeln konstruieren und entsprechende Körpererweiterungen erhalten.
Beispiel: Konstruktione von √z für z=r·cis(φ) (r∈ℝ):
√z=√r·cis(φ/2) bzw. √z=√r·cis(φ/2+180°)
(f) Mit diesen Konstruktionen sind alle Konstruktionen mit Zirkel und Lineal erfaßt.

Zusammenfassung

Ein Punkt x∈ℂ in der komplexen Zahlenebene ist mit Zirkel und Lineal dann und nur dann konstruierbar, wenn es eine Folge von Körpererweiterungen von K0=ℚ(i) gibt mit K0 ⊆K1=K0(√a1) ⊆K2=K1(√a2) ⊆... ⊆Kn =Kn-1(√an) gibt so, dass x∈Kn=ℚ(i,a1,a1,...,an) ist, wobei a1∈K0 , a2 ∈K1, ... , an∈Kn-1 ist. 

Grad(K ,K   )=2 (2≤j≤n), falls a  keine Quadratzahl in K    ist.
      j  j-1                    j                       j-1  

                               k
auf jeden Fall ist Grad(K ) = 2  für ein k∈ℕ.
                         n
Satz: Die Menge der konstruierbaren Punkte in in ℂ ist ein Körper.
Hinweis: Mit Zirkel und Lineal heißt: Das Lineal darf keine Markierungen besitzen. Wie man mit Zirkel und Lineal Senkrechte und Parallelen zeichnet und Strecken mit dem Zirkel übeträgt, wird als bekannt vorausgesetzt.
Bemerkungen: Alle konstruierbaren Punkte sind algebraisch.
Der Grad des Minimalpolynoms eine konstruierbaren komplexen Zahl hat den Grad 2n.
* Die drei Konstruktioneprobleme des klassischen Altertums. Siehe hier
Delische Problem (einfach, da [ℚ(∛2):ℚ]=3)
Einschub: Was sind algebraische und transzendente Zahlen?
Quadratur des Kreises (einfach, da Lindemann bewies, dass π transzendent ist).
Dreiteilung des Winkels. (g28)
Aus Wikipedia: Dreiteilung des Winkels: Ein Winkel mit dem Gradmaß 60° kann mit Zirkel und Lineal konstruiert werden, da cos(60°)=1/2, aber nicht in drei gleiche Teile geteilt werden. Wäre dieser Winkel – also 20° – konstruierbar, dann könnte man auch die reelle Zahl ξ=cos(20°) konstruieren. Für jeden Winkel α gilt das Additionstheorem cos(3α)=4(cos(α))3-3cos(α). Also löst unsere Zahl ξ die Gleichung 1/2=4x3-3x und ist daher eine Nullstelle von p(x)=8x3-6x-1. Da dieses Polynom über ℚ irreduzibel ist (sonst hätte es eine Nullstelle in ℚ), ist [ℚ(ξ):ℚ]=3.
Das Polynom p hat keine Wurzel w=z/n in ℚ, denn dann müßte z=±1 und n=1,2,4 oder 8 sein, was durch Nachrechnen keine Nullstelle ergibt.
Dreiteilung als Neusis-Konstruktion.

Siehe g03.php g51.php

Läßt man weiter Kontruktionsschritte wie die Technik des Papierfaltens oder Neusis-Knstruktionen zu zu so sind zumindest die Winkeldreiteilung und die Duplikation des Volumens eines Würfels lösbar. (Siehe Diplomarbeit von Denise MESIC an der Karl-Franzens-Universität in Graz.)