Der Aufbau der Mathematik - ein Crashkurs

Die Peano-Axiome definieren die natürlichen Zahlen ℕ

(Axiom 1) 1∈ℕ (Oft beginnt ℕ auch mit 0)
(Axiom 2) Es gibt eine bijektive Nachfolgerfunktion n→n+1 von ℕ auf ℕ\{1} für das folgende Induktionsaxiom gilt:
(Axiom 3, genannt das Induktionsxiom)

Wenn X⊆ℕ und 1∈ℕ und mit n∈ℕ auch n+1∈ℕ für alle n∈ℕ, dann ist X=ℕ.

Bemerkung: Eigentlich ist die Addition n+1 noch gar nicht definiert. Die Addition wird später definiert. Exakt müsste man von der Nachfolgerfunktion n→n' statt n→n+1 sprechen.
Weiterlesen: Die vollständige Induktion.

Die ganzen Zahlen ℤ

Wir definieren für jede natürliche Zahl n∈ℕ\{0} ein neues Zeichen -n und setzten ℤ={... -4,-3,-2,-1,0,1,2,3,4,...}

Die Rationalen Zahlen ℚ

In der Produktmengemenge ℤxℤ ist (a,b)∼(c,d) ⇔ ad = bc eine Äquivalenzrelation.

                                          a   c
(Im Grunde bedeutet ad = bc die Beziehung — = —. Aber hier werden die Brüche erst definiert.) 
                                          b   d

                                             a
ℚ ist dann die Menge aller Äquivalenzklassen — = {(c,d)∼(a,b)|c,d∈ℤ}, wobei a,b∈ℤ.
                                             b

Die reellen Zahlen ℝ

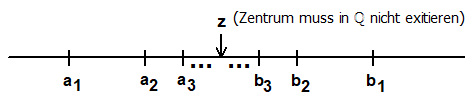Eine "Intervallschachtelung" [a_n,b_n], n∈ℕ, a_n∈ℚ und b_n∈ℚ, ist
eine Folge von Intervallen mit a_n‹b_n mit
a₁≤a₂≤a₃... und ...b₃≤b₂≤b₁ (also die a_n werden immer größer und die b_n immer kleiner)
und für alle ε›0 existiert ein n∈ℕ so, dass b_n-a_n‹ε.
(Es kann sein, dass in ℚ kein Zentrum z der Intervallschachtelung existiert. Zentrum bedeutet: a_n≤z≤b_n fü alle n∈ℕ.)
Zwei Intervallschachtelungen [a_n,b_n] und [c_n,d_n]heißen äquivalent, wenn sie auf dasselbe Zentrum zusteuern, d.h. für alle n∈ℕ existiert m∈ℕ so, dass [a_n,b_n] ⊆ [c_m,d_m] und für alle n∈ℕ existiert m∈ℕ so, dass [c_n,d_n] ⊆ [a_m,b_m].
Die Äquivalenzklassen bilden dann die reellen Zahlen ℝ.

Abzählbar - überabzählbar

Eine Menge heißt abzählbar, wenn es eine bijektive Abbildung von ℕ auf M gibt.
ℕ, ℤ und ℚ sind abzählbar, ℝ ist nicht abzählbar, also überabzählbar.

Die Mengenlehre wurde nach Entdeckung von Widersprüchen axiomatisiert

Georg Cantor definierte

„Unter einer ‚Menge‘ verstehen wir jede Zusammenfassung M von bestimmten wohlunterschiedenen Objekten m unserer Anschauung oder unseres Denkens (welche die ‚Elemente‘ von M genannt werden) zu einem Ganzen."

Und schaffte damit von 1874 bis 1897 eine großartige Grundlegung der Mathematik mit den bekannten Mengen ℕ, ℤ, ℚ, ℝ, ℂ und viele andere.
Es stellte sich heraus, dass seine naive Mengenlehre Widersprüche aufwies.

Die Menge M={x|x∉x} aller Mengen, die sich nicht selbst als Element enthalten

führt zu der Antinomie (publiziert 1903 von n Bertrand Russell): M∈M ⇒ M∉M und M∉M ⇒ M∈M. Was ist also wahr?

---

Grundlage aller Mathematik, die sich mit Zahlen beschäftigt, sind die natürlichen Zahlen ℕ, die durch die Peano-Axiome definiet werden.

ZFC

Die heutige Mathematik, die überwiegend an der Universität gelehrt wird, fußt auf dem ZFC-Axiomatik.
Die Zermelo-Fraenkel-Mengenlehre mit dem Auswahlaxiom (Axiom of Choice) ist nach Ernst Zermelo und Abraham Adolf Fraenkel benannt und wurde in dem ersten Viertel des 20. Jahrhunderts entwickelt.

---

Zum Beispiel gilt in ZFC:
Wenn M eine Menge ist, dann ist auch die Potenzmenge

P(M)={X|X⊆M}

eine Menge. Bei endliche Mengen mit n Elemnten ist die Anzahl der Elemente von P(M) gleich 2ⁿ ist.

Oder: Das (kartesische) Produkt von zwei Menge A und B ist definiert als AxB={(a,b)|a∈A und b∈B}, als Menge aller geordneter Paare (a,b). Damit kann man zum Beispiel beweisen, dass jeder Vektorraum (auch ein unendlich dimensionalen Vektorraum) eine Basis hat.