Die Homepage von Joachim Mohr
Körpererweiterungen
Körpererweiterungen spielen in der Mathematik eine wichtige Rolle, da sie das Verständnis von algebaischen Strukturen wesentlich vertieft.Körperrweiterungen finden sich bei folgenden Theorien.
-
Bekannt sind als Körpererweiterungen des Körpers ℚ der rationalen Zahlen der Körper ℝ der reellen Zahlen und der Körper ℂ der komplexen Zahlen, die in der Analysis eine grroße Rolle spielen.
- Der Köper ℝ der reellen Zahlen ist dadurch charakterisiert, dass jede Intervallschachtelung ein Zentrum besitzt. Er ist deshalb volltändig. Während die Menge der rationlen Zahlen abzählbar ist, ist die Menge der reellen Zahlen überabzälbar.
- Der Körper ℂ der komplexen Zahlen ist darüber hinaus dadurch charakterisiert, dass jedes Polynom p vom Grad größer 1 mit rationalen, reellen oder komplexen Koeffizienten in ℂ Nullstellen hat, dort sogar in Lineafaktoren zerfällt: p(x)=(x-x1)(x-x2)...(x-xn) (n∈ℕ). Fußnote: In dieser Arbeit ℕ={1,2,3,..} und ℕ0={0,1,2,3,..}.
- In der Galoistheorie spielen Körpererweterungen eine Schlüsselrolle bei der Frage nach der Lösbarkeit von Polynomgleichungen mt Radiklen.
- Die Frage, ob Konstruktionsaufgaben mit Zirkel und Lineal möglich sind, werden mit Hilfe des Begriffs der Körpereweiterung gelöst.
- In der Zahlentheorie untersucht man die Eigenschaften von ganzen Zahlen und ihren algebraischen Erweiterungen, insbesondere den algebraischen Zahlkörpern. Die Eigenschaften von Primzahlen, quadratischen Zahlkörpern und diophantischen Gleichungen werden oft mit Hilfe von Körpererweiterungen analysiert.
Hier werden zunächst Körper zwischen dem Körper ℚ der rationalen Zahlen und ℂ der komplexen Zahlen behandelt. Es sind dann Erweiterungskörper von ℚ.
Definition: Eine Menge K mit ℚ⊆K⊆ℂ heißt Erweiterungskörper von ℚ, wenn K selbst ein Köper ist, wenn also gilt:
a,b∈K ⇒ a+b∈K und a∈K ⇒-a∈K
a,b∈K ⇒ a·b∈K und a∈K ⇒a-1∈K
Dann sind (K,+) und (K\{0},·) kommutative Gruppen und für (K,+,·) ist auch das Distributivgesetz erfüllt.
Jede Körpererweiterung K mit Charakteristik 0 kann als Vektorraum über ℚ betrachtet werden. Der Grad der Körpererweiterung ist dann die Dimension von K. Allgemein:
Definition: Seien K und L Körpererweiterungen von ℚ. Dann kann L als Vektorraum über K betrachtet werden. Der Grad von L über K ist dann die Dimension von L als Vektorraum über K. Der Grad wird mit [L:K] bezeichnet.
L ist dann eine Erweiterungskörper von K. Solch eine Erweierungskörper über K wird mit L/K bezeichnet.
(Die Schreibweise L/K für zwei Körper K und L ist ist historisch bedingt und besagt nur dass L ein Erweiterungskörper von K ist, dagegen ist zum Beispiel ℤ/5ℤ eine mathematische Konstruktion für den Körper, dessen Elemente die Nebenlassen 0+5ℤ, 1+5ℤ, ,,,, 4+5ℤ von 5ℤ sind.)
Beispiel 1: ℂ ist eine Körpererweiterung über ℝ vom Grad 2, da {1,i} eine Basis von ℂ über ℝ ist.
ℂ={a+bi|a,b∈ℝ}
Beispiel 2:Wir betrachten den kleinsten Körper über ℚ, der zusätzlich noch √2 enthält: K ist dann der Durchschnitt aller Teilkörper von ℚ, die √2 enthalten. Man bezeichnet dann diesen Körper als ℚ(√2)="Q adjungiert √2".
Behauptung: {1,√2} ist Basis von ℚ(√2), d.h. Es gilt ℚ(√2)={a+b√2|a,b∈ℚ}. Der Grad von ℚ(√2) ist also 2.
Beweis: Die einzig nichttriviale Behauptung betrifft das Inverse der Multiplikation.
Wir bestimmen für a,b∈ℚ das Inverse (a+b√2)-1 von a+b√2 (a≠0 oder b≠0).
Beispiel 3: Werden weitere Quadratwurzeln adjungiert, erhöht sich der Grad um den Faktor 2.
Berechnung des Inversen von 1-√2+i-√2i:
(1-√2+i-√2i)*(a+b√2+ci+d√2i)=1 ergibt ein Lineare Gleichunssystem mit der Lösung
Beispiel 5: Die Körpererweiterung ℚ(i)={a+bi|a,b∈ℚ} wird als Gaußscher Zahlkörper bezeichnet. Er hat den Grad [ℚ(i):ℚ]=2, denn {1,i} ist Basis des Vektorraumes ℚ(i) über ℚ. Es ist ähnlich wie beim vorhergehenden Beispiel
Satz: Sind M/K und L/M zwei Körpererweiterungen, also K⊆M⊆L, dann ist [L:K] = [L:M]·[M:K].
Beispiel 2:Wir betrachten den kleinsten Körper über ℚ, der zusätzlich noch √2 enthält: K ist dann der Durchschnitt aller Teilkörper von ℚ, die √2 enthalten. Man bezeichnet dann diesen Körper als ℚ(√2)="Q adjungiert √2".
Behauptung: {1,√2} ist Basis von ℚ(√2), d.h. Es gilt ℚ(√2)={a+b√2|a,b∈ℚ}. Der Grad von ℚ(√2) ist also 2.
Beweis: Die einzig nichttriviale Behauptung betrifft das Inverse der Multiplikation.
Wir bestimmen für a,b∈ℚ das Inverse (a+b√2)-1 von a+b√2 (a≠0 oder b≠0).
-1 1 a-b√2 a-b√2 a -b
(a+b√2) = —————— = —————————————— = ———————— = ———————— + ———————√2 = c+d√2
a+b√2 (a+b√2)(a-b√2) 2 2 2 2 2 2
a - 2b a - 2b a - 2b
a -b
für c= ———————— ∈ℚ und d= ————————∈ℚ.
2 2 2 2
a - 2b a - 2b
Beispiel 3: Werden weitere Quadratwurzeln adjungiert, erhöht sich der Grad um den Faktor 2.
— — — — —
ℚ(√2,√3)={a+b√2+c√3+d√6|a,b,c,d∈ℚ} hat den Grad 4 über ℚ.
- - - - - -
Das Inverse von zum Beispiel 3+5√2-7√3+11√6 ist -3681/89234-2773/89234√2+2563/89234√3+2755/89234√6.
Beispiel 4: Das Inverse von 1-√2+i-√2i
Der Körper ℚ(i,√2)={a+b√2+ci+d√2i|a,b,c,d∈ℚ} hat die Dimesion 4 über ℚ. Die Basisielemente {1,√2,i,√2i} sind linear unabhängig. Das Inverse ist also eindeutig bestimmt:Berechnung des Inversen von 1-√2+i-√2i:
(1-√2+i-√2i)*(a+b√2+ci+d√2i)=1 ergibt ein Lineare Gleichunssystem mit der Lösung
1 1 1 1
a= - — -, b= - —, c= —, d= —
2 2 2 2
-1 1
Also: (1-√2+i-√2i) = —(-1-√2+i+√2i)
2
Beispiel 5: Die Körpererweiterung ℚ(i)={a+bi|a,b∈ℚ} wird als Gaußscher Zahlkörper bezeichnet. Er hat den Grad [ℚ(i):ℚ]=2, denn {1,i} ist Basis des Vektorraumes ℚ(i) über ℚ. Es ist ähnlich wie beim vorhergehenden Beispiel
-1 a -b
(a+bi) = —————— + ———————i ∈ℚ(i).
2 2 2 2
a + b a + b
Beispiel 6: ℚ(i,√2) hat als Erweiterungskörper von ℚ(√2) den Grad [ℚ(i,√2):ℚ(√2)]=2, denn
-1 a+c√2 b+d√2 2 2
(a+bi+c√2+d√2i) = ————— + i————— für z=(a+c√2) + (b+d√2)
z z
Nach dem folgenden Satz ist [ℚ(i,√2):ℚ]=4 mit ℚ(i,√2)={a+bi+c√2+d√2i|a,b,c,d∈ℚ}.
Beweis: Ist {d1,d2, ..., dk} eine Basis des Vektorraumes M über K und {e1,e2, ..., en} eine Basis des Vektorraumes L über M,
dann kann man zeigen, dass {ei·dj|i=1,2,...,k, j=1,2,..,n} eine Basis von L/K ist, also [L:K]=n·k=[L:M]·[M:K] ist ∎
Eine Körpererweiterung heißt normal, wenn jedes Polynom mit Nullstellen in L alle seine Nullstellen in L hat.
Weitere Körpererweiterungen
L=ℚ(∛2)= {a+b∛2+c∛4|a,b,c∈ℚ} ... [L:ℚ]=3.
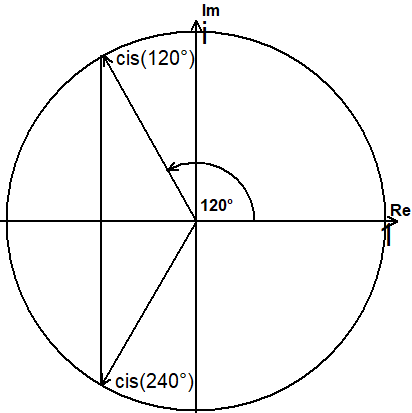
L ist nicht normal, denn das Polynom p=X3-2 hat nur die Nullstelle ∛2 in L, nicht aber seine beiden komplexen Nullstellen ∛2·cis(120°) und ∛2·cis(240°).
L=ℚ(∛2,cis(120°) ist dagegen normal und [L:ℚ]=[L:ℚ(∛2]·[ℚ(∛2:ℚ]=2·3=6.
Eine Basis des Vektorraumes L über ℚ ist {1,∛2, ∛4, cis(120°), ∛2·cis(120°), ∛4·cis(120°)}.
L=ℚ(∛2)= {a+b∛2+c∛4|a,b,c∈ℚ} ... [L:ℚ]=3.
L ist nicht normal, denn das Polynom p=X3-2 hat nur die Nullstelle ∛2 in L, nicht aber seine beiden komplexen Nullstellen ∛2·cis(120°) und ∛2·cis(240°).
L=ℚ(∛2,cis(120°) ist dagegen normal und [L:ℚ]=[L:ℚ(∛2]·[ℚ(∛2:ℚ]=2·3=6.
Eine Basis des Vektorraumes L über ℚ ist {1,∛2, ∛4, cis(120°), ∛2·cis(120°), ∛4·cis(120°)}.
Mit Zirkel und Lineal konstrierbare Punkte
Ausgehend von den Punkten 1 und i in der Ebene ℚ(i) kann man alle Punkte, die die Addition, Suntraktion, Multiplikation und Division betreffen, mit Zirkel und Lineal konstruieren. Mann kann jedoch auch Quadratwurzeln konstruieren. Es gilt:Ein Punkt x∈ℂ in der komplexen Zahlenebene ist mit Zirkel und Lineal dann und nur dann konstruierbar, wenn es eine Folge von Körpererweiterungen von K0=ℚ(i) gibt mit K0 ⊆K1=K0(√a1) ⊆K2=K1(√a2) ⊆... ⊆Kn =Kn-1(√an) gibt so, dass x∈Kn=ℚ(i,a1,a1,...,an) ist, wobei a1∈K0 , a2 ∈K1, ... , an∈Kn-1 ist. Jede der Körpererweiterungen K2/K1, K3/K2, ..., Kn/Kn-1 hat den Grad 1 oder den Grad 2. Es gilt also für einen mit Zirkel und Lineal konstruirbar Punkt x, dass [ℚ(x):ℚ]=2k für k∈ℕ ist.
Da ein Würfel mit dem Volumen 2 die Seitenlänge ∛2 hat und ℚ(∛2)={a+b∛2+c∛4|a,b,c∈ℚ] mit [ℚ(∛2):ℚ]=3 ist, folgt: Ein Würfel mit dem dopplten Volumen als dem Einheitswürfel kann nicht mit Zirkel und Lineal konstruiert werden (Delisches Problem).
Ähnlich kann man beweisen, dass die Dreiteilung eines Winkels und die Quadratur des Kreises nicht immer mit Zirkel und Lineal möglich ist.
3— 1 1 —
Sei b=√2 = 1,44... und ς=cis(120°)=cos(120°)+isin(120°) = -— + i—√3.
2 2
2
(ς und ς = cis(240°) sind die komplexen, nicht reellen 3. Einheitswurzeln.
 2
und b, b·ς und b·ς alle drei komplexen 3. Wurzeln von 2.
2
Dann ist der Grad von ℚ(b)={x+y·b+z·b |x,y,z∈ℚ} über ℚ gleich 3
und der Grad von ℚ(b,b·ς)=ℚ(b,ς) über ℚ(b) gleich 2, also
der Grad von ℚ(b,ς) über ℚ gleich 6.
2
und b, b·ς und b·ς alle drei komplexen 3. Wurzeln von 2.
2
Dann ist der Grad von ℚ(b)={x+y·b+z·b |x,y,z∈ℚ} über ℚ gleich 3
und der Grad von ℚ(b,b·ς)=ℚ(b,ς) über ℚ(b) gleich 2, also
der Grad von ℚ(b,ς) über ℚ gleich 6.
Definition: Ein Element a∈L in einer Körpererweiterung L/K heißt algebraisch über K, wenn es die Nullstelle eine Polynoms aus K[X]\{0} ist, sonst transzendent.
Beispiel 1: i ist algebraisch über ℚ, da es Nullstelle des Polynoms X2+1=0 ist.
Beispiel 2: √a (a∈ℚ, a positiv oder negativ) ist algebraisch, da √a Nullstelle des Polynoms X2-a ist.
Beispiel 3: Die k-te Einheitswurzel ζ ist algebraisch über ℚ, da ζ Nullstelle des Polynoms Xk-1 ist (k=2,3,...)
Beispiel 4: π=3.14159265... ist transzendent. Beweis 1882 von Ferdinand von Lindemann.
e=1+1/1!+1/2!+1/3!+... ist transzendent Beweis 1873 von Charles Hermite, 1873.
Satz: Sei a algebraisch über K, dann gilt K(a)={anan+an-1an-1+...+a0|
an,an-1,...,a0∈K}, wobei das Minimalpolynom von a, d.h. das kleinste Polynom, das a als Nullstelle hat, den Grad n besitzt
(n∈ℕ).
{1,a,a2,...,an-1} ist dann eine Basis von K(a).
Beispiel 2: √a (a∈ℚ, a positiv oder negativ) ist algebraisch, da √a Nullstelle des Polynoms X2-a ist.
Beispiel 3: Die k-te Einheitswurzel ζ ist algebraisch über ℚ, da ζ Nullstelle des Polynoms Xk-1 ist (k=2,3,...)
Beispiel 4: π=3.14159265... ist transzendent. Beweis 1882 von Ferdinand von Lindemann.
e=1+1/1!+1/2!+1/3!+... ist transzendent Beweis 1873 von Charles Hermite, 1873.
Aufgabe: Zeige a=√2+√3 ist algebraisch über ℚ und bestimme das Minimalpolynom von a.
Lösung:
a=√2+√3
a2= 5 + 2√2·√3
(5-a2)^2=24
a4-10a2+1=0
Das Mnimalpolynom ist p=x4-10x2+1.
Somit hat ℚ(a)={a+b√2+c√3+d√6|a,b,c,d∈ℚ} den Grad 4 über ℚ.
Man kann zeigen dass der Körper aller algebraischer Zahlen über ℚ abzählbar ist, die Menge der reellen Zahlen ℝ jedoch überabzählbar. Folglich ist
auch die Menge der transzendenen Zahlen überabzählbar.
Lösung:
a=√2+√3
a2= 5 + 2√2·√3
(5-a2)^2=24
a4-10a2+1=0
Das Mnimalpolynom ist p=x4-10x2+1.
Somit hat ℚ(a)={a+b√2+c√3+d√6|a,b,c,d∈ℚ} den Grad 4 über ℚ.
Algebraische Körpererweiterungen
Siehe Distler: S. 19
Sei α algebraisch über ℚ und L=ℚ(α) und sei f das Minimalpolynom von α.Satz: ℚ(α) ist isomorph zu ℚ[X]/(f), dem Polynomring ℚ[X] "modulo f".
Beispiel: ℚ(√2) und ℚ[X]/(X2-2)
Etwa: (3+5√2)≙(3+5X), (4+7√2)≙(4+7X), wobei mod f gerechnet wird, d.h. X2=2
Einerseits ist (3+5√2)(4+7√2)=(82+41√2), andererseits (3+5X)(4+7X)=(12+35X2)+41X=(82+41X).
Etwa: (3+5√2)≙(3+5X), (4+7√2)≙(4+7X), wobei mod f gerechnet wird, d.h. X2=2
Einerseits ist (3+5√2)(4+7√2)=(82+41√2), andererseits (3+5X)(4+7X)=(12+35X2)+41X=(82+41X).
4 2
Beispiel: Das Minimalpolynom von ℚ(√2,√3) ist f=X - 10X + 1 mit den Nullstellen
x =±√2±√3.
1,2,3,4
2 3
ℚ(√2,√3)={a+b√2+c√3+d√6|a,b,c,d∈ℚ}=ℚ/(f)={a+bX+cX +dX |a,b,c,d∈ℚ; mod (f)}
2 3 2 3
Sei A=1+3X+X + 5X und B=2+X+3X + X . Dann ist
2 3 4 5 6
AB=2+7X+8X +21X +11X +16X +5X.
4 2 4 2
Modulo f gerechnet ist X - 10X + 1=0, also X =10X -1
5 3 6 4 2 2
entsprechend X =10X - X und X = 10X - X =99X - 10.
2 3
⇒ AB=-59-9X+613X +181X . Allgemein:
2 3 2 3 2 3
(a+bX+cX +dX )(e+fX+gX +hX )=p+qX+rX +sX (nämlich) =
(ae-bh-cg-ch-de-10dh)+(ae+be-dg)X+(ag+be+10bh+ce+10cg+10ch+10de+99dh)X2+(ah+bg+ce+de+10dg)X3 .
Quelle S. 26
Satz 3.14
Siehe dazu
auch youtube
Teil I
Teil II
ℚ(√2) ≌ (isomorph) ℚ[X]/(X2-2)
Zwei Polynome in ℚ[X]/(X2-2)={a+bX|a,b∈ℚ} sind äquivalent, wenn sie bei Divisiondurch X2-2 denselben Rest haben.
Zum Beispiel ist (a+bX)(c+dX)=ac+adX+bcX+bdX·X. Da aber X2=2 folgt (a+bX)(c+dX)=ac+2bd+(ad+bc)X.
Zum Vergleich (a+b√2)(c+d√2)=ac+2bd+(ad+bc)√2 (a,b∈ℚ).
φ:a+b√2→a+bX (a,b∈ℚ) ist der gesuchte Isomorphismus.
Beispiel K=ℚ3
Mit der Vektorraumaddition(a,b,c)+(d,e,f)=(a+d,b+e,c+f) und der Multiplikation nach dieser Definition
(a,b,c)·(d,e,f)=(ad+2bf-2ce,ae-bd+2cf,af+be+cd).
Das Nullelement ist (0,0,0) und das Einselement ist (1,0,0).
Berechnung von (0,1,0)·(0,1,0)·(0,1,0).
Zunächst (0,1,0)·(0,1,0)=(0,0,1), dann (0,1,0)·(0,1,0)·(0,1,0)=(0,0,1)·(0,1,0)=(-2,0,0).
Das Element (0,1,0) entspricht also ∛-2 und (0,0,1) entspricht ∛4.
K ist also isomorph zu V={a+b∛-2+c∛4|a,b,c∈ℚ}⊂ℂ.
K enthält als kleinsten Körper {(a,0,0)|a∈ℚ} isomorph zu ℚ.
Zunächst (0,1,0)·(0,1,0)=(0,0,1), dann (0,1,0)·(0,1,0)·(0,1,0)=(0,0,1)·(0,1,0)=(-2,0,0).
Das Element (0,1,0) entspricht also ∛-2 und (0,0,1) entspricht ∛4.
K ist also isomorph zu V={a+b∛-2+c∛4|a,b,c∈ℚ}⊂ℂ.
Der Körper V={a+b∛-2+c∛4|a,b,c∈ℚ}
Bestimmung des Minimalpolynoms
Sei α=∛-2. Dann ist α2=∛4 und α3=-2, also α3+2=0. Das Minimalpolynom ist also f=X3+2. Nach Eisenstein ist es irreduzibel.
Bestimmung des Zerfällungskörpers eines Polynoms. Quelle F12T1A5 (a)
Zerfällungskörper des Polynoms x5+5
k
(a) Die Nullstellen des Polynoms sind ζ ·α (k=0,1,2,3,4)
5— 5 5
mit ζ = cis(72°) und α = √5cis(36°) mit ζ = 1 und α = -1.
5— 5— 5— 5— 5— 5—
x = √5cis(36°), x = √5cis(108°), x =√5cis(180°)=-√5, x = √5cis(252°), x = √5cis(324°)
1 2 3 4 5
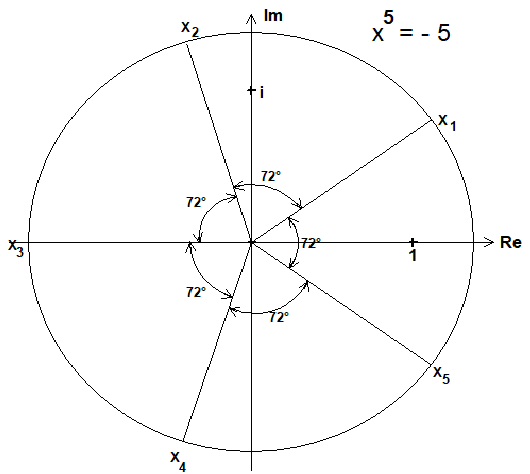
Der Zerfällungskörper ist K=ℚ(α,ζ).
b) Das Polynom f=X5+5 ist normiert und nach Eisenstein irreduzibel (p=5).
K=Gal(f,ℚ) ist galoisch.
f ist das Minimalpolynom von α über ℚ ⇒ [ℚ(α),ℚ] = grad(f) = 5.
4 3 2
Das Minimalpolynom von ζ ist das fünfte Kreisteilungspolynom Φ = x + x + x + x + 1
5
⇒[Q(ζ) : Q] = grad(Φ ) = ϕ(5) = 4.
5
Folglich: [K:Q] = [K:Q(α)]·[Q(α):Q] = 4 · 5 = 20 (Ausführlic: Siehe Quelle)
c) G=Gal(K/Q)=Gal(f,Q) ⊆ S5 hat 20 Elemente.
