Die Homepage von Joachim Mohr
Quelle: K. Schmidt, 2023
Die Konstruktion des n-Ecks ist identisch mit der Konstruktion von Einheitswurzeln.Einheitswurzeln
Beispiel: n=5 Gesucht: Lösungen von x5=1
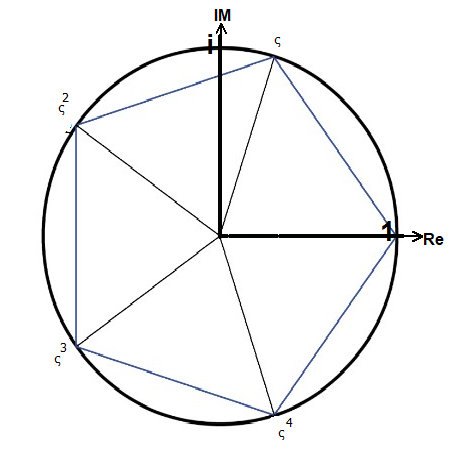
Das regelmäßige 5-Eck
ς=cis(72°)=cos(72°)+isin(72°)
2
ς =cis(144°)
3
ς =cis(216°)
4
ς =cis(288°)
5 0
ς =cis(360°)=ς =1
5
{x∈ℂ|x =1} = {1,ς,ς2,ς3,ς4}
2πi
für ς=cis(72°)=cos(72°)+isin(72°)=exp(———)
5
Die 5. Einheitswurzeln G={1,ς,ς2,ς3,ς4} bilden bez. der Multplikation ein Gruppe, die isomorph zu additiven Gruppe
ℤ5=ℤ/5ℤ bezüglich der Isomorphie σ(n)=ςn
(n∈{
0,
1
2
3
4} ist.
Hier erzeugen alle Elemente ≠ 1 die Gruppe G=‹ς›=‹ς2›=‹ς3›=‹ς4›, da φ(5)=4 (φ=Eulersche Funktion).
Beispiel: n=9 Gesucht: Lösungen von x9=1
 Die Löungen der
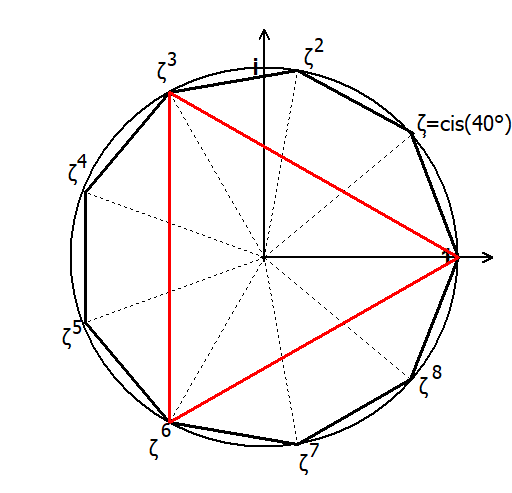
Die Löungen der Gleichung x9=1 sind die Einheitswurzeln
1, ς=cis(40°), ς2, ς3, ς4, ς5, ς6, ς7 und ς8
cos(40°)≈0,766... ist nicht mit Zirkel und Lineal konstruierbar,
denn x=cos(40°) ist Lösung einer Gleichung 3. Grades
(8x3-6x+1=0) und diese Gleichung hat einen
Zerfällungskörper L mit Grad(L,ℚ)=3
——————
1 —
cis(40°)= — ∛-4+4i√2
2
Die Gruppe mit 9 Elementen
G={1, ς, ς2, ς3, ς4, ς5, ς6, ς7, ς8} ist zyklisch: G=‹ς›=‹ς2›=‹ς4›=‹ς5 ›=‹ς7›=‹ς8›.
Man nennt die Elemente von G primitiv, wenn sie die ganze Gruppe erzeugen.
Ihre Anzahl ist φ(9)=6 (φ=Eulersche Funktion). Da φ(9) keine 2-er Potenz ist, ist das 9-Eck nicht mit Zirkel und Lineal konstruierbar (siehe unten).
Eine Untergruppe von G mit 3 Elementen ist U={1,ς3,ς6}
Eine Näherungskontruktion des 9-Ecks mit Zirkel und Lineal des Winkels mit 40° kann zum Beispiel mit arctan(5/6)=39,8° oder mit cos(40°)=0,766≈3/4 erfolgen.
Allgemeines n-Eck
Sei n≥3 und C={x∈ℚ|xn=1} die Menge der n Einheitswurzeln über ℚ.Eine primitive Einheitswurzel in C={1,ζ,ζ2,...,ζn-1} ist eine Element, das C erzeugt. Das sind die Elemente ζm∈C mit ggT(m,n)=1. Ihre Anzahl ist φ(n) (φ: Eulersche Funktion).
(FLA 404) Ein wichtiges Problem ist die Berechnung des Körpergrades [ℚ(ζ):ℚ]. Dies ist der Grad des Minimalpolynoms Φ∈ℚ[X]. Ist nämlich [ℚ(ζ):ℚ] eine Potenz von 2, dann ist das n-Eck mit Zirkel und Lineal konstruierbar.
Das Minimalpolynom Φ ist das Produkt aller Linearfaktoren (X-z), wobwi z eine primitive Einheitswurzel ist.
Satz: Grad(Φ)=φ(n) (langer Beweis).
Folgerung: Ist φ(n) eine Potenz von 2, dann ist das n-Eck mit Zirkel und Lineal konstruierbar.
n.k.= nicht mit Zirkel und Lineal konstr.
Φ = x - 1 φ(1)=1
1
Φ = x+1 φ(2)=1
2
2
Φ = x +x+1 φ(3)=2
3
2
Φ = x +1 φ(4)=2
4
4 3 2
Φ =x +x +x +x+1 φ(5)=4
5
2
Φ =x -x+1 φ(6)=2
6
6 5 4 3 2
Φ =x +x +x +x +x +x+1 φ(7)=6 n.k.
7
4
Φ =x +x+1 φ(8)=4
8
6 3
Φ =x +x +1 φ(9)=6 n.k.
9
4 3 2
Φ =x -x +x -x+1 φ(10)=4
10
10 9
Φ =x + x + ... + 1 φ(11)=10 n.k.
11
4 2
Φ = x - x +1 φ(12)=4
12
...
48 7
Φ =x +...+2x -... +1 φ(105)=48 n.k.
105
Konstruktion von Vielecken
Das n-Eck ist konstruierbar, wenn ζn=cis(360°/n) bzw. cos(360°/n) konstruierbar ist.Konstruktion des Fünfecks mit Zirkel und Lineal
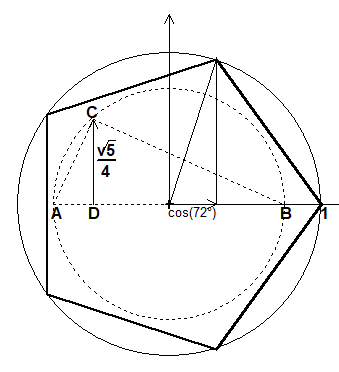 Im rechtwinkigen Dreieck ABC sind die
Im rechtwinkigen Dreieck ABC sind die
Hypothenusenabschnitte
1 5
p=AD=— und q=DB=— und damit
4 4
—— √5
die Höhe h=DC = √pq = —— ,
4
also "mit Zirkel und Lineal" auch
√5-1
cos(72°)= ———— konstruierbar.
4
Und damit kann das 5-Eck im
Einheitskreis konstruiert werden.
Satz: Das n-Eck ist genau dann konstruierbar, wenn die Eulersche Funktion φ(n)=Grad[cis(360°/n):Q] eine Potenz von 2 ist. (siehe Gradmann S.45)
Da φ(17)=16=24 ist, ist das 17-Eck konstruierbar.
Formel von Gauß:
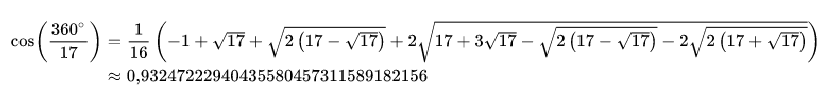
Satz: Ein n-Eck kann man nur dann mit Zirkel und Lineal konstruieren,
- wenn φ(n) eine Potenz von 2 ist oder
- wenn n das Produkt einer Potenz von 2 mit verschiedenen Fermatschen Primzahlen ist.
Beweis: Tutorium S. 252
In der Zeichnung rechts, wird das Fünfeck um 120° und 240° gedreht, was mit Zirkel und Lineal möglich ist.
Eine Primzahl ist eine Fermatsche Primzahl, wenn sie von der Form 22k+1 für ein eine natürliche Zahl k ist. Man vermutet, dass nur die ersten 5 Fermatschen Zahlen
- 220+1 =3,
- 221+1 = 5,
- 222+1 = 17,
- 223+1 = 257 und
- 224+1 = 65537
225+1=4294967297 ist keine Primzahl (Leonhard Euler errechnete 1732, dass 4294967297=641·6700417)
Mehr darüber:
g34.php
Zu den mit Zirkel und Lineal konstruierbaren Vielecken gehören:
- a) Das 4-Eck, 8-Eck, 16-Eck, ...
- b) Das 3-Eck, 6-Eck, 12-Eck, ...
- c) Das 5-Eck, 10-Eck, 20, Eck
- b) und c) kombiniert: Das 15-Eck, 30-Eck, 60-Eck, ...
- d) Das 17-Eck, 34-Eck, 68-Eck, ...
- u.s.w.
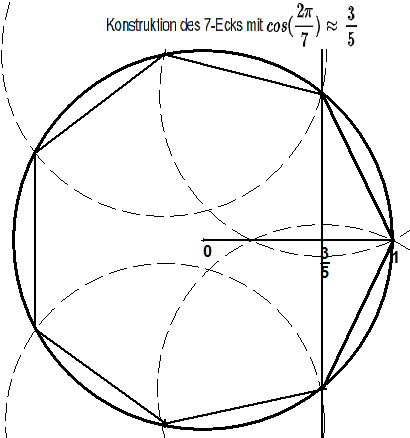
Das 7-Eck
Die Einheitswurzel des 7-Ecks berechnet sich zu ζ=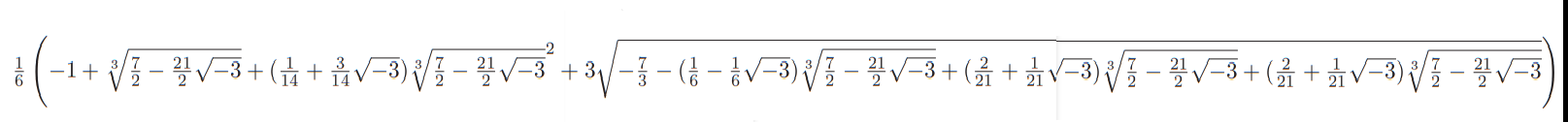
 Das 7-Eck und das 9-Eck usw. ist also nicht mit Zirkel und Lineal konstruierbar, wohl aber Näherungen, man muss nur
cos(360°/7) und cos(360°/9) durch Brüche annähern.
Das 7-Eck und das 9-Eck usw. ist also nicht mit Zirkel und Lineal konstruierbar, wohl aber Näherungen, man muss nur
cos(360°/7) und cos(360°/9) durch Brüche annähern.
Mit der Methode des Kettenbruchs ist zum Beispiel:
7-Eck mit cos(360°/7)=0,623489801. Näherung: 3/5=0,6; besser 5/8=0,625 noch besser 48/77=0,6234.
Hier in der Zeichnung isr der einfachse Näherungswert 3/5 gewählt.
Verbindet man die Endpunkte dieses 5-Ecks mit O(0|0), so betragen rechnerisch die Innenwinkel gegenüber der 1., 2, 3., 5.,6. und 7. Seite α=arctan(4/3)≈51,42°. Der Innenwinkel gegenüber der 4. Seite aber β=360°-6·arctan(4/3)≈53,13°
Die 4. Seite ist 3% größer als die anderen.
