Die Homepage von Joachim Mohr
Gleichung 4. Grades. - Sonderfälle
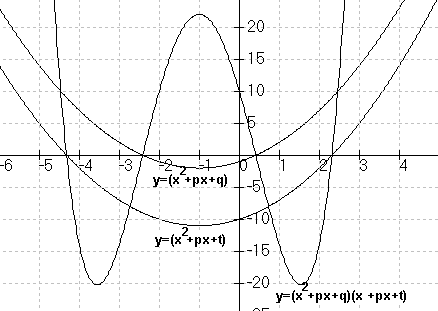
Zerlegung: x4+ax3+bx2+cx+d=(x2+px+q)(x2+sx+t)
Zurück:
Gleichungen 4. Grades , allgemein.
Hier werden Sonderfälle der Gleichung 4. Grades x4 + ax3 + bx2 + cx + d = 0 mit einfacher Lösungsformel vorgestellt:
Sonderfall I 4ab-a3=8c (Das Schaubild ist symmetrisch)
Sonderfall II c=0 und 4b=a2
Sonderfall III p=s mit weiteren Sonderbedingungen
Sonderfall IV q=t
Sonderfall V Symmetrische Gleichung
Sonderfall VI Biquadratische Gleichung x4 + bx2 + d = 0 (a=0 und c=0)
I Sonderfall 4ab-a3=8c oder 2p-a=0
Das Schaubild der Funktion x->x4+ax3+bx2+cx+d ist symmetrisch zu der Geraden mit der Gleichung x = - a/4 parallel zur y-Achse.Substituiert man x = u - a/4, erhält man eine biquadratische Gleichung der Form u4+b'u2+d'=0
Kurzfassung:
In diesem Fall lautet die Lösung
a
p = -
2
————————
1 /2 2
q = -(c + \/c - a d
a
a
s = -
2
————————
1 /2 2
t = -(c - \/c - a d
a
Lösung kopierbar: p=1/2*a q=1/a*(c+sqrt(c^2-a^2*d) oder q=c/a+sqrt(c^2/a^2-d) s=1/2*a t=1/a*(c-sqrt(c^2-a^2*d) oder t=c/a-sqrt(c^2/a^2-d) x1=-p/2+sqrt((p/2)^2-q) x2=-p/2-sqrt((p/2)^2-q) x3=-s/2+sqrt((s/2)^2-t) x4=-s/2-sqrt((s/2)^2-t)Bemerkung: 4ab-a3-8c ist invariant gegenüber linearen Transformationen, d.h.
aus (u-t)4+a1(u-t)3+b1(u-t)2+c1(u-t)+d = x4+ax3+bx2+cx+d für x= u-t
folgt 4a1b1 - a13 - 8c1 = 4ab - a3 - 8c
Ausführlich:
Beipiele: x^4+4x^3+6x^2+4x+1=0 a=4 b=6 c=4 Hier: 4ab-a3=8c (=32) x^4+2x^3-11x^2-12x+36=0 a=2 b=-11 c=-12 Hier: 4ab-a3=8c (=-96)
Im Rechenschema des allgemeinen Falles wird bei der Berechnung von
q durch (-a+2p) dividiert.
Es darf also bei der Rechnung dort nicht sein, dass a=2p ist.
Im Fall a=2p ist dann p=s=a/2 und c=1/2ab-1/8a3 bzw.4ab-a3=8c.Die Berechnung von p, q, r und s sowie der Nullstellen ist dann kurz:
Nämlich: p=1/2*a; s=1/2*a; q=(4*b-a^2+sqrt(a^4-8*a^2*b+16*b^2-64*d))/8; t=(4*b-a^2-sqrt(a^4-8*a^2*b+16*b^2-64*d))/8; x1=-p/2+sqrt((p/2)^2-q); x2=-p/2-sqrt((p/2)^2-q); x3=-s/2+sqrt((s/2)^2-t); x4=-s/2-sqrt((s/2)^2-t);Und: Das Schaubild ist dann symmetrisch zu einer Parallelen der y-Achse.
Herleitung:
Aus x4+a*x3+b*x2+cx+d=(x2+px+q)(x2+sx+t) folgt:
a=p+s, b=q+ps+t,c=qs+pt, d=qt. Mit a=2p und s=p folgt:
a=2p, b=p^2+q+t, c=pq+pt, d=qt. Weitere Umformungen:
p=a/2, b=1/4a^2+q+t, c=1/2aq+1/2at.
Die zweite Gleichung nach t aufgelöst und in die dritte eingesetzt:
t=b-1/4a^2-q, c=1/2aq+1/2a(b-1/4a^2-q)=1/2ab-1/8a^3 q.e.d
a=p+s, b=q+ps+t,c=qs+pt, d=qt. Mit a=2p und s=p folgt:
a=2p, b=p^2+q+t, c=pq+pt, d=qt. Weitere Umformungen:
p=a/2, b=1/4a^2+q+t, c=1/2aq+1/2at.
Die zweite Gleichung nach t aufgelöst und in die dritte eingesetzt:
t=b-1/4a^2-q, c=1/2aq+1/2a(b-1/4a^2-q)=1/2ab-1/8a^3 q.e.d
Und: q ist dann Lösung der Gleichung: 4q^2+(a^2-4b)q+4d=0
Berechnung mit Maple
Eine weiter Vereinfachung ergibt sich mit den Beziehungen
f:=x->x^4+a*x^3+b*x^2+(4*a*b-a^3)/8*x+d;
g:=x->x^2+p*x+q; s:=a-p; t:=b-q-a*p+p^2;h:=x->x^2+s*x+t;
r:=x->((4*a*b-a^3)/8-b*p+a*p^2-p^3-a*q+2*p*q)*x+(d-b*q+q^2+a*p*q-p^2*q);
simplify(f(x)-g(x)*h(x)-r(x));#Ergebnis 0
solve({(4*a*b-a^3)/8-b*p+a*p^2-p^3-a*q+2*p*q=0,d-b*q+q^2+a*p*q-p^2*q=0},{p,q});
#ein Ergebnis:p=1/2a; 4q^2+(a^2-4b)q+4d=0
Probe:
p:=1/2*a; q:=(4*b-a^2+sqrt(a^4-8*a^2*b+16*b^2-64*d))/8;
s:=1/2*a; t:=(4*b-a^2-sqrt(a^4-8*a^2*b+16*b^2-64*d))/8;
c:=(4*a*b-a^3)/8;
f:=x->x^4+a*x^3+b*x^2+(4*a*b-a^3)/8*x+d;
g:=x->x^2+p*x+q; h:=x->x^2+s*x+t;
r:=x->(c-b*p+a*p^2-p^3-a*q+2*p*q)*x+(d-b*q+q^2+a*p*q-p^2*q);
simplify(r(x));#Ergebnis:0
3
4ab-a = 8c
4 2 2 2 - 2 -
und a - 8ab + 16b - 64d = (a - 4b + 8\/d)·(a - 4b - 8\/d)
Daraus folgt:
——————
/ 2 ——————
c / c 1 /2 2
q = - + \/ —— - d = -(c + \/c - a d )
a 2 a
a
——————
/ 2 ——————
c / c 1 /2 2
t = - - \/ —— - d = -(c - \/c - a d
a 2 a
a
Kopierbar:
q=c/a+sqrt(c^2/a^2-d)
t=c/a-sqrt(c^2/a^2-d)
Hier das Rechenschema zur Berechnung aller Nullstellen in Maple:
f:=x->x^4+a*x^3+b*x^2+1/8*(4*a*b-a^3)*x+d; p:=1/2*a; q:=(4*b-a^2+sqrt(a^4-8*a^2*b+16*b^2-64*d))/8; s:=1/2*a; t:=(4*b-a^2-sqrt(a^4-8*a^2*b+16*b^2-64*d))/8; g:=x->(x^2+p*x+q)*(x^2+s*x+t);simplify(f(x)-g(x));#Probe stimmt! x1:=-1/4*a+1/4*sqrt(3*a^2-2*sqrt(a^4-8*a^2*b+16*b^2-64*d)-8*b); x2:=-1/4*a-1/4*sqrt(3*a^2-2*sqrt(a^4-8*a^2*b+16*b^2-64*d)-8*b); x3:=-1/4*a+1/4*sqrt(3*a^2+2*sqrt(a^4-8*a^2*b+16*b^2-64*d)-8*b); x4:=-1/4*a-1/4*sqrt(3*a^2+2*sqrt(a^4-8*a^2*b+16*b^2-64*d)-8*b); h:=x->(x-x1)*(x-x2)*(x-x3)*(x-x4); simplify(f(x)-h(x));#Probe stimmt
Beispiel zum Sonderfall c=(4ab-a^3)/8
Kurze Rechnung
a) f(x)=x4+4x3+6x2+4x+1
a=4 b=6 c=4 // =(4ab-a^3)/8 d=1 p=1/2*a=2 s=1/2*a=2 q=(4b-a^2+sqrt(a^4-8a^2*b+16b^2-64d))/8=1 t=(4b-a^2-sqrt(a^4-8a^2*b+16b^2-64d))/8=1 x1=-p/2+sqrt((p/2)^2-q)=-1 x2=-p/2-sqrt((p/2)^2-q)=-1 x3=-s/2+sqrt((s/2)^2-t)=-1 x4=-s/2-sqrt((s/2)^2-t)=-1
b) f(x)=x4+2x3-11x2-12x+36
a=2 b=-11 c=-12 d=36 p=1/2*a=1 s=1/2*a=1 q=(4*b-a^2+sqrt(a^4-8*a^2*b+16*b^2-64*d))/8=-6 t=(4*b-a^2-sqrt(a^4-8*a^2*b+16*b^2-64*d))/8=-6 x1=-p/2+sqrt((p/2)^2-q)=2 x2=-p/2-sqrt((p/2)^2-q)=-3 x3=-s/2+sqrt((s/2)^2-t)=2 x4=-s/2-sqrt((s/2)^2-t)=-3
c) f(x)=x4+4x3-11x2-30x+50
a=4
b=-11
c=-30
d=50
Probe:
c=(4*a*b-a^3)/8=-30
q ist Lösung der Gleichung 4q^2+(a^2-4b)q+4d=0
p=1/2a=2
s=1/2a=2
q=(4b-a^2+sqrt(a^4-8a^2*b+16b^2-64d))/8=-5
t=(4b-a^2-sqrt(a^4-8a^2*b+16b^2-64d))/8=-10
x1=-p/2+sqrt((p/2)^2-q)=sqrt(6)-1
x2=-p/2-sqrt((p/2)^2-q)=-1-sqrt(6)
x3=-s/2+sqrt((s/2)^2-t)=sqrt(11)-1
x4=-s/2-sqrt((s/2)^2-t)=-1-sqrt(11)
f(x)=x4+6x3+9x2+1
Rechnung: a=6 b=9 c=0 d=1 p=1/2*a=3 q=(4*b-a^2+sqrt(a^4-8*a^2*b+16*b^2-64*d))/8=1*i s=1/2*a =3 t=(4*b-a^2-sqrt(a^4-8*a^2*b+16*b^2-64*d))/8=-1*iAlso ist f(x)=x^4+6x^3+9x^2+1 = (x^2+3x+i)·(x^2+3x-i)
Man sieht hier: Im Sonderfall ist q nicht immer reell (da q Lösung einer quadratischen Gleichung ist), aber die Zerlegung gelingt trotzdem. Und die Nullstelle lassen sich berechnen:
x1 = -3/2-1/4*sqrt(18+2*sqrt(97))-1/4*I*sqrt(-18+2*sqrt(97))
x2 = -3/2+1/4*sqrt(18+2*sqrt(97))+1/4*I*sqrt(-18+2*sqrt(97))
x3 = -3/2-1/4*sqrt(18+2*sqrt(97))+1/4*I*sqrt(-18+2*sqrt(97))
x4 = -3/2+1/4*sqrt(18+2*sqrt(97))-1/4*I*sqrt(-18+2*sqrt(97))
Die Zerlegung in reelle quadratische Faktoren ist:
(x-x1)·(x-x3)=x^2+(3+1/2*sqrt(18+2*sqrt(97)))*x
+9/4+3/4*sqrt(18+2*sqrt(97))+1/4*sqrt(97) und
(x-x3)·(x-x4)=x^2+(3-1/2*sqrt(18+2*sqrt(97)))*x
+9/4-3/4*sqrt(18+2*sqrt(97))+1/4*sqrt(97)
II Unterfall c=0 und 4b=a2
Wir ersetzten a durch 2a und kommen dann auf die Form:
/———————————————————————\
| 4 3 2 2 |
| x + 2ax + a x + d = 0 | (Der Koeffizient vor x ist Null)
\———————————————————————/
Dann ergibt sich für die Zerlegung
4 3 2 2 2 2
x + 2ax + a x + d = (x + px +q)(x + sx + t)
—— ——
mit p=a, s=a, q = \/-d, t= -\/-d
Dies erkennt man sofort durch Einsetzen und Ausmultiplizieren.
Rechenschema für Maple:
p:=a;
s:=a;
q:=sqrt(-d);
t:=-sqrt(-d);
x1:=-p/2+sqrt((p/2)^2-q);
x2:=-p/2-sqrt((p/2)^2-q);
x3:=-s/2+sqrt((s/2)^2-t);
x4:=-s/2-sqrt((s/2)^2-t);
Beispiel
4 3 2
x - 6x + 9x - 3 = 0;
kopierbar:
x^4-6*x^3+9*x^2-3=0
- -
Lösung: p=-3, s=-3, q= \/3 t= - \/3
x1 = 3/2+1/2*sqrt(9-4*sqrt(3))=2,219686871
x2 = 3/2-1/2*sqrt(9-4*sqrt(3))=0,780313129
x3 = 3/2+1/2*sqrt(9+4*sqrt(3))=3,495507657
x4 = 3/2-1/2*sqrt(9+4*sqrt(3))=-0,495507657
III Sonderfall p=s mit weiteren Sonderbedingungen
(x^2+p*x+q)*(x^2+s*x+t)= x^4+a*x^3+(1/4*a^2+t+q)*x^2+1/2*a*(t+q)*x+q*tKann ich bei der Gleichung x4+ax3+bx2+cx+d
den letzten Koeefizienten d zerlegen in d=q*t und ergibt sich, dass
b=1/4*a^2+t+q und c=1/2*a*(t+q) ist, dann ist p=s=a/2 und die Zerlegung bereits bekannt.
Beispiel x4+4x3+12x2+16x+15
Man probiert für d=15=3·5 die Lösung q=3 und t=5. Probe:b=1/4*a^2+t+q=12
c=1/2*a*(t+q)=16 Stimmt (zufällig)
Somit mit p=s=a/2
x4+4x3+12x2+16x+15=(x2+2x+3)·(x2+2x+5)
IV Sonderfall q=t
Zerlegung: x4+ax3+bx2+cx+d=(x2+px+q)(x2+sx+t)
Diesen Fall erkennt man an folgender Beziehungc = a·sqrt(d)
Die Gleichung können wir dann auch mit d= q2 in folgender Form angeben.
/———————————————————————————\
| 4 3 2 2 |
| x + ax + bx + aqx + q = 0 |
\———————————————————————————/
Dann folgt: a=p+s und b=2q+ps
Daraus kann man p und s berechnen:
——————————— ————————————
1 2 1 2
p= -(a + \/a - 4b + 8q) s = -(a - \/a - 4b + 8q) t=q
2 2
Probe mit Maple: p:=1/2*a+1/2*sqrt(a^2-4*b+8*q); s:=1/2*a-1/2*sqrt(a^2-4*b+8*q); yp:=expand((x^2+p*x+q)*(x^2+s*x+q)); #Ergebnis yp=x^4+a*x^3+b*x^2+a*q*x+q^2
Beispiel x4+3x3-14x2+6x+4=0
kopierbar: x^4+3*x^3-14*x^2+6*x+4=0In diesem Fall ist a=3, b=-14, c=6 und d=4 ist die Bedingung c=a*sqrt(d) erfüllt.
Mit q=t=2 ergibt sich p=6 s=-3
x1=-3+sqrt(7)
x2=-3-sqrt(7)
x3=1
x4=2
Beispiel x4+2x3+3x2+4x+4=0
kopierbar: x^4+2*x^3+3*x^2+4*x+4=0In diesem Fall ist a=2, b=3, c=4 und d=4 ist die Bedingung c=a*sqrt(d) erfüllt.
Mit q=t=2 ergibt sich p und s zu
p=1+sqrt(2) und s=1-sqrt(2)
Die vier Lösungen der Gleichung x4+2x3+3x2+4x+4=0 sind also
x1=(-1/2-1/2*sqrt(2))+(sqrt(5/4-1/2*sqrt(2)))*I;
x2=(-1/2-1/2*sqrt(2))-(sqrt(5/4-1/2*sqrt(2)))*I;
x3=(1/2*sqrt(2)-1/2)+(sqrt(1/2*sqrt(2)+5/4))*I;
x4=(1/2*sqrt(2)-1/2)-(sqrt(1/2*sqrt(2)+5/4))*I;
Maple kann diese Gleichung nicht lösen.
V Unterfallfall: Symmetrische Gleichung
Eine Gleichung 4. Grades der folgenden Form nennt man symmetrisch.4 3 2 x + ax + bx + ax + 1 = 0Dies ist ein Unterfall von Sonderfall IV und die folgende Zerlegung sofort berechenbar:
4 3 2 2 2
x + ax + bx + ax + 1 = (x + px + 1)·(x + sx + 1)
——————————— ——————————
1 2 1 2
p = -(a+\/ a - 4b + 8) s = -(a - \/a - 4b + 8)
2 2
kopierbar: p=1/2*a+1/2*sqrt(a^2-4*b+8) und s=1/2*a-1/2*sqrt(a^2-4*b+8)
Beispiel x4+4x3-12x2+4x+1=0
Kopierbar: x^4+4*x^3-12*x^2+4*x+1=0Daraus ergibt sich p=2+3*sqrt(2) q=1, s==2-3*sqrt(2), t=1 und damit
x1=-1-3/2*sqrt(2)+1/2*sqrt((2+3*sqrt(2))^2-4)=-0,164524665 x2=-1-3/2*sqrt(2)-1/2*sqrt((2+3*sqrt(2))^2-4)=-6.078116021 x3= -1+3/2*sqrt(2)+1/2*sqrt((2-3*sqrt(2))^2-4)= 1.628626278 x4= -1+3/2*sqrt(2)-1/2*sqrt((2-3*sqrt(2))^2-4)=0,6140144080
Beispiel x4+2x3-14x2+2x+1=0
kopierbar: x^4+2*x^3-14*x^2+2*x+1= 0
p = 1+sqrt(17)
q = 1
s = 1-sqrt(17)
t = 1
x1 = -1/2-1/2*sqrt(17)+1/2*sqrt(14+2*sqrt(17)) = -0,203258342
x2 = -1/2-1/2*sqrt(17)-1/2*sqrt(14+2*sqrt(17)) = -4,919847284
x3 = -1/2+1/2*sqrt(17)+1/2*sqrt(14-2*sqrt(17)) = 2,760905633
x4 = -1/2+1/2*sqrt(17)-1/2*sqrt(14-2*sqrt(17)) = 0,362199993
(Nicht lösbar bei Maple)
VI Unterfallfall: a=0 und c=0
Eine Gleichung 4. Grades der folgenden Form nennt man häufig biquadratische Gleichung4 2 x + bx + d = 0Es handelt sich hier um eine quadratische Gleichung für x2 und die vier Lösungen ergeben sich sofort durch die bekannten Formeln.
———————
———— b / b 2
x = ± \/w für w = - - ± \/ (-) - d
1,2,3,4 1,2 1,2 2 2
—————
Die Berechnung komplexer Quadratwurzeln \/a+b·i = x + y·i
wird hier ausführlich besprochen.
Die Zerlegung
4 2 2 2 x + bx + d = (x + px +q)(x + sx + t)ergibt sich sodann durch
p = -(x + x ), q = x ·x
1 2 1 2
s = -(x + x ), t = x ·x
3 4 3 4
wobei die Nullstellen beliebig permutiert werden können,
was bei rellem b, d und gewünschten reellen p, q, r und s wichtig wird.
Beispiel x4+4x2+1=0 (b2 - 4d > 0)
Mit x1= sqrt(-2+sqrt(3)) = (1/2*sqrt(6) - 1/2*sqrt(2))*i x2= - sqrt(-2+sqrt(3)) = - (1/2*sqrt(6) - 1/2*sqrt(2))*i x3= sqrt(-2-sqrt(3)) = (1/2*sqrt(2) + 1/2*sqrt(6))*i x4= - sqrt(-2-sqrt(3)) = - (1/2*sqrt(2) + 1/2*sqrt(6))*i ergibt sich mit p= -(x1+x2) etc. p=0 q=2-sqrt(3) s=0 t=2+sqrt(3) alsox4+4x2+1=(x2+2-√3)(x2+2+√3)
Beispiel x4+x2+4=0 (b2 - 4d < 0)
Mit x1= 1/2*sqrt(-2+2*i*sqrt(15)) = 1/2*sqrt(3) + 1/2*sqrt(5)i x2= -1/2*sqrt(-2+2*i*sqrt(15)) = -1/2*sqrt(3) - 1/2*sqrt(5)i x3= 1/2*sqrt(-2-2*i*sqrt(15)) = 1/2*sqrt(3) - 1/2*sqrt(5)i x4= -1/2*sqrt(-2-2*i*sqrt(15)) = -1/2*sqrt(3) + 1/2*sqrt(5)i ergibt sich mit p = -(x1+x3) etc. p=-sqrt(3) q=2 s=sqrt(3) t=2 alsox4+x2+4=(x2-√3x+2)(x2+√3x+2)
Direkte Berechnung von reellem p,q,r und t aus reellen b≠0 und d≠0.
x^4+b*x^2+d =(x^2+p*x+q)*(x^2+s*x+t) ergibt das Gleichungssystem:
s+p = 0
t+p*s+q =b
p*t+q*s=0
q*t = d
Man kann q≠0 voraussetzen und erhält sofort die zwei Bedingungen:
t=d/q und s=-p
und damit
p*(d-q^2)=0 und d/q-p^2+q=b
Falls d < 0 oder 4*d < b^2 < 0 ergibt sich
p=0, q=1/2*b+1/2*sqrt(b^2-4*d), s=0, t=1/2*b-1/2*sqrt(b^2-4*d)
Sonst ergibt sich
q=sqrt(d), p =sqrt(2*sqrt(d)-b), s=-sqrt(2*sqrt(d)-b), t=sqrt(d)
Weiter Fallunterscheidungen wegen des Wurzelvorzeichens entfallen,
da dann nur die Werte von p,q und s und t vertauscht werden.
Beispiel a) b=1 d=4
=> p=sqrt(2*sqrt(d)-b)=sqrt(3), q=sqrt(d)=2,
s= -sqrt(3), t=2
Beispiel b) b=4 d=1
=> p=0, q=1/2*b+1/2*sqrt(b^2-4*d)=2+sqrt(3),
s=0, t=2-sqrt(3)
Beispiel c) b=1 d=-4
=> p=0, q=1/2*b+1/2*sqrt(b^2-4*d)=1/2+1/2*sqrt(17),
s=0, t=-1/2*sqrt(17)+1/2
Beispiel d) b=4 d=-1
=> p=0 q=1/2*b+1/2*sqrt(b^2-4*d)=2+sqrt(5),
s=0, t=3-sqrt(5)
