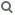Die vollständige Induktion
Ein Crashkurs
Diese Datei kann auch als PDF-Datei heruntergeladen werden. Download ....
Die vollständige Induktion, ein Thema der höheren Mathematik, ist unverzichtbarer Inhalt beim Mathematik-, Physik- und Ingenieurstudium.
Sie eignet sich nicht zum Schulstoff, da das Verständnis für die verwendete Logik und ihre axiomatische Grundlegung fehlt. Demotivierend für die Studierenden ist außerdem, dass damit Formeln bewiesen, aber nicht hergeleitet werden. Die Formeln fallen einfach vom Himmel. Trotzdem findet die vollständige Induktion von Fall zu Fall Eingang in den Lehrplan der Gymnasien oder - und das ist für mich der Anlass dieses Kurses - der Aufnahmeprüfungen für das Hochschulstudium für Ausländer. Sie wird als Kapitel für sich behandelt und hat im Schulstoff keine weiteren Anwendungen.
Der folgende Kurs soll - ganz im Gegensatz zu den sonstigen
Intentionen dieser Seiten - nicht überzeugen, sondern nur die nötigen
Techniken vermitteln, um eine Prüfung einigermaßen unbeschadet zu
überstehen.
Er kann vielleicht sogar bewirken, dass der Leser ein Vergnügen an diesem
Thema und anderen Beweistechniken, die eine solide logische Schulung
erfordert, empfindet.
Wer sich in die vollständige Induktion vertiefen möchte, findet einen ersten Einstig im Wikipedia-Lexikon.
Im folgenden ist N = {1;2;3;4; ... } die Menge der natürlichen Zahlen und N0 = {0;1;2;3;4; ...}.In manchen Büchern wird die Null zu N hinzugenommen. Im Wesentlichen ändert sich nichts dadurch.
Mit Hilfe der vollständigen Induktion werden Aussageformen A(n) bewiesen (n ε N).
(Näheres zu Aussageformen siehe unten.)
Wir werden weiter unten die folgende Formel mit Hilfe der vollständigen Induktion beweisen:
n·(n+1)
A(n): 1 + 2 + 3 + ... + n = ——————— (Eine Summe als "geschlossener Ausdruck")
2
Gewöhnlich spricht man hier von einer Formel und meint damit die
Allgemeingültigkeit einer Aussageform. Dies wird noch erläutert.Wie man auf diese Formel kommt, wird hier nicht besprochen. Es geht nur darum, ihre Gültigkeit nachzuweisen. (Würde ich nämlich die Formel auf direktem Wege herleiten, wäre es ja nicht mehr nötig, sie zu beweisen. Also tun wir so, irgend jemand hätte die Formel als Behauptung aufgestellt. Jetzt geht es nur noch darum, sie zu beweisen.)
Für jedes nεN wird die Aussageform zu einer Aussage:
1·(1+1)
A(1): 1 = ——————— (wahr: Probe stimmt)
2
2·(2+1)
A(2): 1 + 2 = ——————— (wahr: Probe stimmt)
2
3·(3+1)
A(3): 1 + 2 + 3 = ——————— (wahr: Probe stimmt)
2
...
1000000·1000001
A(1000000): 1 + 2 + ... + 1000000 = ——————————————— (Bitte nachrechnen :-)
... 2
An diesem Beispiel erkennt man: Aussageformen enthalten eine oder
mehrere Variablen (hier die Variable nεN). Sie werden zu
Aussagen, wenn die Variablen bestimmte Werte annehmen. Jede Aussage ist
entweder wahr oder falsch.Hier sind Aussageformen der Form A(n) wichtig, die für alle n ε N wahr sind. Diese Aussageformen nennt man allgemeingültig in N.
1. Aufgabe: Sind die folgenden Aussageformen in N allgemeingültig?
a) Wenn n ein Vielfaches von 6 ist, dann ist n eine gerade Zahl.
b) Wenn n = 0 ist, dann ist n + 1 = 1.
c) Wenn n = n + 1 ist, dann ist n + 1 = n + 2.
Lösungen
Die vollständige Induktion ist eine Beweistechnik, um die Formeln der Form A(n) zu beweisen.
"Formeln der Form A(n)" bedeutet - allgemeiner formuliert -: "Die Allgemeingültigkeit der Aussageform A(n) für nεN oder "Die Gültigkeit der Aussage A(n) für alle nεN."
Beweisschema der
|
| Die Formel A(n) soll bewiesen werden. |
| Der Beweis erfolgt in zwei Schritten. |
| I Induktionsanfang: Prüfe, ob A(1) gilt. |
|
II Induktionsschritt: Zeige: A(n) => A(n+1) (n ε
N) ("Aus A(n) kann A(n+1) hergeleitet werden") |
| Mit dem Nachweis von I und II ist die Formel A(n) bewiesen. |
Zur Begründung verweise ich auf die Dominosteine in der Figur am Anfang des Kapitels.
Beispiel: Behauptung:
n·(n+1)
A(n): 1 + 2 + 3 + ... + n = ———————
2
Beweis: I Induktionsanfang:
1·(1+1)
A(1): 1 = ——————— (wahr: Probe stimmt)
2
II Induktionsschritt: Wir nehmen an:
n·(n+1)
A(n): 1 + 2 + 3 + ... + n = ——————— gälte
2
Jetzt müssen wir zeigen, dass daraus die Formel
(n+1)·(n+2)
A(n+1): 1 + 2 + 3 + ... + n + (n+1) = ———————————
2
hergeleitet werden kann.Herleitung:
n·(n+1)
Aus 1 + 2 + 3 + ... + n = ——————— folgt
2
durch Addition von n+1 auf beiden Seiten:
n·(n+1)
1 + 2 + 3 + ... + n + (n + 1) = ——————— + (n+1)
2
Jetzt werden die Rechnungen meist sehr technisch. Du musst
darauf hinsteuern, dass als letzter Ausdruck der Gleichungskette die rechte
Seite von A(n+1) steht.
Wenn Du aber in der Prüfung das Schema soweit aufgeschrieben hast, hast Du
die meisten Punkte schon erworben.
n·(n+1) + 2·(n+1)
=> 1 + 2 + 3 + ... + n + (n + 1) = ————————————————— |(n+1) ausklammern!
2
(n+2)·(n+1)
=> 1 + 2 + 3 + ... + n + (n + 1) = ———————————
2
∎
2. Aufgabe: Beweise:
n n+1
a) 1 + 2 + 4 + 8 + ... + 2 = 2 - 1
1 1 1 1 1
b) 1 + - + - + - + ... + —— ≥ 1 + n·-
2 3 4 n 2
2
Lösung3. Aufgabe: Schreibe jeweils A(1) und A(n+1) auf: (Das ist schon der halbe Beweis.)
a) Eine arithmetische Reihe
2
1 + 3 + 5 + ... (2n - 1) = n
b) Noch eine arithmetische Reihe:
n·(n+1)
5 + 8 + 11 + 14 + ... + (5+3·n) = 5(n+1) + 3———————
2
c) Die allgemeine arithmetische Reihe:
n·(n+1)
a + (a+k) + (a + 2k) + (a + 3k) + ... + (a + nk) = a(n+1) + k———————
2
d) Die allgemeine geometrische Reihe;
n+1
2 3 n 1 - x
a + ax + ax + ax + ... + ax = a·————————
1 - x
e) n = n + 1 (Zusatzfrage: Warum nicht allgemeingültig!)
2 2 2 2 1
f) 1 + 2 + 3 + ... + n = -n·(n + 1)·(2n + 1)
6
Nebenbei bemerkt: Weitere Summenformeln
g) 3n - 3 ist durch 6 teilbar
h) Die Bernoulliesche Ungleichung
Ein Beispiel, bei dem der Induktionsanfang n=2 ist.
n
(1+p) > 1 + n·p für p > -1 und n > 1
x
i) Für f(x) = (x+2)·e ist die n-te Ableitung
(n) x
f (x) = (x + n + 2)·e
-x
j) Für f(x) = (x+2)·e ist die n-te Ableitung
(n) n -x
f (x) =(-1) (x + 2 - n)·e
Lösungen4. Aufgabe: Beweise, dass die Aussageformen von Aufgabe 2 bis auf e) allgemeingültig sind
(Vor allem sind wichtig: a) d) i) und j).
Lösungen
5. Aufgabe: (Diesmal beginnt die Folge mit n=0)
Die Folge (a ) wird rekursiv definiert durch
n
a = a
0
a = r·a + s für n ≥ 0 (r ≠ 1)
n+1 n
Behauptung: Für die Folge gibt es einen geschlossenen Ausdruck der Form
n
a = c·r + d (n ≥ 0) für passende Zahlen c und d.
n
Bemerkung: Die wichtigste Anwendung hiervon ist die Tilgung eines
Darlehens, siehe ...Lösung
6. Aufgabe: Nur für Geübte und Kenner von Rechnungen mit Binomialkoeffizienten.
Die Binomialkoeffizienten werden definiert zu:
n n·(n-1)·(n-1)·...·(n-k+1) ( ) = —————————————————————————— (kεN , nεR) [Zähler und Nenner haben k Faktoren) k 1 · 2 · 3 · ... ·k 0Man beachte bei dieser Definition, dass n keine natürliche Zahl sein muss, zum Beispiel ist
-1/2 (-1/2)·(-3/2)·(-5/2)·(-7/2) 1·3·5·7 35
( ) = —————————————————————————— = —————————— = ———
4 1 · 2 · 3 · 4 1·2·3·4·16 128
n
Bemerkung: ( ) = 1, das neutrale Element der Multiplikation.
0
2k k -1/2
Behauptung: ( ) = (-4) ·( ) (kεN )
k k 0
Lösung
Hinweis: Damit lässt sich die folgende Formel beweisen:
n 0 2n 2 2n-2 4 2n-4 2n-2 2 2n 0
4 = ( )·( ) + ( )·( ) + ( )·( ) + ... + ( )·( ) + ( )·( )
0 n 1 n-1 2 n-2 n-1 1 n 0
n
2k 2n-2k
= Σ ( )·( )
k n-k
k=0
Eine Formel über die mittleren Elemente des Pascalschen Dreiecks
siehe "Concrete Mathematics" (5.39) von Graham, Knuth und Patashnik.
Beweis: Wir verwenden die "Vandermondesche Identität":
k
m n m+n
Σ ( )·( ) = ( )
j k-j k
j=0
m+n
( ) ist nämlich die Anzahl aller Teilmengen mit k Elementen aus einer Menge
k
mit m+n Elementen. Spaltet man dann die Menge in zwei Mengen mit m und n Elementen auf
so erhält man die Anzahl aller Teilmengen mit k Elementen, indem man aus der ersten Menge
j Elemente wählt und aus der zweiten k-j und alle Anzahlen von j=0 bis k addiert.
Die Formel gilt auch für reelle Zahlen m und n.
Damit folgt:
n n
2k 2n-2k k n-k -1/2 -1/2
Σ ( )·( ) =Σ(-4) ·(-4) ·( )·( )
k n-k k n-k
k=0 k=0
k -1 k (-1)·(-2)·...·(-n) n
=(-4) ·( ) = (-4) ·—————————————————— = 4
n 1 · 2 · n
∎ (Jutta Gut)