Joachim Mohr Mathematik Musik Delphi
 |
Einführung in das Skalarprodukt |

|
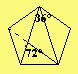
Mit TTMathe "Geometrie|Vektor/Zwei Vektoren/Dreieck" kontrolliert: - —— —— 1 a) 5; 6,5; 5; \/5; 2\/10 b) 3; 7; 11; 13; \/14 4·12 - 3·5 6 - 8 + 5 2 a) cosα = —————————— => α = 59,5° b) cosα = ————————— => α = 83,9° 5·13 —— —— \/21·\/38 3. | 8| |4| |-4| ——> | | ——> | | ——> | | —— —— BC = |-3| AC = |0| AB = | 3| a= \/82 b = 4 c =\/34 | | | | | | |-3| |0| | 3| α = 133,3° β = 18,7° γ = 27,9°
-> -> -> -> -> ->
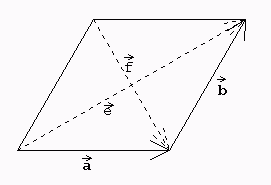
Im Parallelogramm sei e = a + b und f = a - b .
2 ->2 2 ->2
Wir verwenden die Gleichheit a = a bzw. b = b
->2 ->2
und die Äquivalenz a = b <=> a = b .
->2 ->2 -> ->
4. a) Voraussetzung: a = b Behauptung: e · f = 0
-> -> ->2 ->2
b) Voraussetzung: e ·f = 0 Behauptung: a = b
->2 ->2
Beweis: a = b
-> -> -> -> -> -> ->2 ->2
<=> e · f = (a + b)·(a - b) = a - b = 0
|a| | 2|
5. Ist n = |b| =|-5| und P(p |p |p ) = P(3|-7|11) ε E, dann kann man
|c| | 0| 1 2 2
die Ebenengleichung sofort folgendermaßen angeben:
|x - p | |a| |x - 3| | 2|
-> -> -> | 1 1| | | | 1 | | |
I E: (x - p )·n = 0 => E: |x - p |·|b| = 0 => E: |x + 7|·|-5| = 0
| 2 2| | | | 2 | | |
|x - p | |c| |x - 11| | 0|
| 3 3| | | | 3 | | |
=> E: 2(x -3) + (- 5)(x + 7) + 0(x - 11) = 0 => E: 2x - 5x = 41
1 2 3 1 2
->
II E: ax + bx + cx = d, wobei a,b,c durch n und d durch P bestimmt ist.
1 2 3
Also: E: 2x - 5x = d. Punktprobe mit P(3|-7|11) ergibt 2·3 - 5·(-7) = d
1 2
Somit E: 2x - 5x = 41.
1 2
-> | 0| | 2|
6. g: x = | 8| + t·| 0|
|-11| |-7|
7. E: -x + 2x = - 8
2 3
8. a) gesucht Abstand des Punktes P(-1|2|1) von der Ebene E: 2*x - x - 5x = 3.
1 2 3
-> |-1| | 2|
I. Lösungsweg (ohne Formel): Die Gerade g: x = | 2| + t·|-1| durch P senkrecht zu E
| 1| |-5|
schneidet E im Punkt F(-1/5|1'3/5|-1).
——> 2 ——
dann ist d(P,E) = |FP | = -\/30 = 2,191 LE.
5
II. Lösungsweg: Die Hesse-Form von E: ax + bx + cx - d = 0 ist
1 2 3
ax + bx + cx - d 2x - x - 5x - 3
1 2 3 1 1 3
———————————————— = 0. Hier ——————————————— = 0.
————————————— ——
/2 2 2 \/30
\/a + b + c
P(p |p |p ) = P(-1|2|1) hat dann von E den Abstand d = d(P,E)
1 2 3
| ap + bp + cp - d| | |
| 1 2 3 | |2·(-1) - 2 - 5 - 3| 12 2 ——
d = | ————————————————| Hier d= |——————————————————| = ———— = -\/30 LE
| ———————————— | | —— | —— 5
| /2 2 2 | | \/30 | \/30
|\/a + b + c |
(Kontrollrechnung mit TTMathe "Geometrie|Abstand Punkt Ebene")
-> |4| |1|
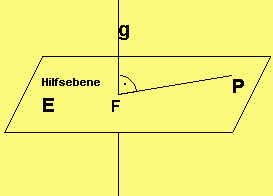
b) Gegeben g: x = |2| + t·|1| und P(4|6|2).
|1| |0|
Gesucht Abstand d = d(P,g). Wir berechnen zunächst mit
der Hilfsebe E: x + x = 10 durch P senkrecht zu g
1 2
den Schnittpunkt F von E mit g. Das führt zur
Gleichung (4+t) + (2 + t) = 10 mit der Lösung
——> |-2|
t = 2 und F(6|4|1) => d = |FP | = || 2|| = 3 LE
| 1|
(Rechnung: TTMathe "Geometrie|Abstand Punkt Gerade")
c) Gesucht: Der Abstand der windschiefen Geraden
-> |8| |3| -> | 7| |3|
g: x = |8| + s·|2| und h: x = | 2| + t·|3|
|5| |2| |10| |4|
-> |a| -> | |3| -> | |3|
1. Schritt: Suche Vektor n = |b| mit n ——— |2| und n ——— |3|.
|c| |2| |4|
Ausrechnen mit Hilfe des Vektorproduktes
-> |3| |3| | 2|
ergibt n = |2|x|3| = |-6|.
|2| |4| | 3|
Ohne Vektorprodukt wird die Lösung des LGS bestimmt:
3a + 2b + 2c = 0 3a + 2b + 2c = 0
( ) <=> ( )
3a + 3b + 4c = 0 b + 2c = 0
2 -> | 2|
c beliebig, b = -2c, a = -c. Eine Lösung genügt. Zum Beispiel n =|-6|
3 | 3|
-> 1 -> 1| 2|
2. Schritt: Bilde den Einheitsvektor: n = ————n = -|-6| .
o |->| 7| 3|
|n |
-> -> -> 1|-1| | 2| 1
3. Schritt: Formel d(g,h) = |(q - p )·n | = -|-6|·|-6| = -(-2 + 36 + 15) = 7 LE
0 7| 5| | 3| 7
Rechnung macht auch TTMathe"Geometrie|Zwei Geraden"
