Joachim Mohr   Mathematik Musik Delphi
≡
Lektion 1   Lektion 2    Lektion 3  Lektion 4   Lektion 5   Lektion 6   Lektion 7   Lektion 8   Lektion 9

1. Lektion: Töne, Intervalle, Frequenzen und Frequenzverhältnisse

Ein Ton kann auf zweierlei Art beschrieben werden:

1. Hörpsychologisch: Als Wahrnehmung eines Tones. 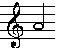Noten spiele den Ton a'


2. Physikalisch: Als Luftschwingungen. Diesen kann man eine Frequenz zuordnen.
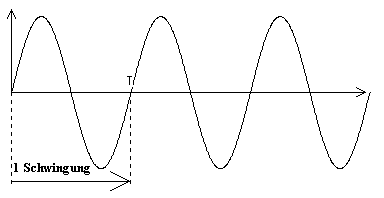schwingung Hier: Ton a'

Frequenz: 440 Schwingungen pro Sekunde

Frequenz: f = 440 Hz (Hertz)

Schwingungsdauer: T = 2,273 ms
Umrechnung: T = 1/f; f = 1/T


Je höher der Ton,
um so höher die Frequenz.
Dies wird hier an der
C-Dur-Tonleiter demonstriert. 		tonleiter spiele Tonleiter


Jedem Ton kann man eine Frequenz zuordnen.
Beispiel: c' (das eingestrichene c) hat die Frequenz 264 Hz, e' die Frequenz 330 Hz, g' die Frequenz 396 Hz und c'' die Frequenz 528 Hz.
Töne kann man in der Höhe unterscheiden. Dabei gilt: Je höher ein Ton erklingt, um so größer ist seine Frequenz.
Durch ein Intervall wird das Nacheinanderausführen oder Zusammenklingen von zwei Tönen beschrieben.

Ein musikalischer Mensch kann das zu zwei Tönen gehörende Intervall ohne Hilfsmittel zuordnen.

Dabei ist es unerheblich, was als erster Ton erklingt.

Zum Beispiel ist das Intervall von c' nach g' dasselbe wie von f' nach c'', nämlich eine Quinte.

Wir werden dafür folgende Schreibweise einführen: Qui = c'g' = f'c''.

Physikalisch wird das Intervall durch das Frequenzverhältnis beschrieben.

Intervall Noten Frequenzverhältnis Hören / Zusammen
Oktav oktav 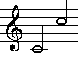528:264=2:1 Oktav
Oktav
Quint quint 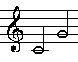396:264=3:2 Quinte
Quinte
Quart quart 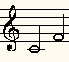352:264=4:3 Quarte
Quarte
große Terz 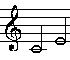grterz 330:264=5:4 große Terz
große Terz


Zu erwähnen bleibt noch die Prim. Das ist das Intervall, bei dem beide Töne gleich sind. Zu hören ist ein Ton, nur etwas lauter.


Diese Intervalle klingen rein, d.h. ohne Schwebungen. Ein Beispiel mit Schwebungen haben Sie in der Einführung schon kennengelernt:

spiele erstes e'', zweites e'' und beide gleichzeitig

Dasselbe noch einmal mit reiner Sinusschwingung (ohne Beimischung von Obertönen) reine Prim, verstimmte Prim
höre auch hier
primreinundunrein

Hier noch weitere Beispiele zu Schwebungen. Bei der Oktave und Quinte wurde die Frequenz des zweiten Tones um 1,5 %) erniedrigt. Achten Sie auch hier auf die Schwebungen.
unreine Oktav
unreine Quinte
unreine Quinte mit verstärktem Differenzton
Beim ersten Lesen können Sie die Eulersche Schreibweise (,e'' = Tiefkomma e'' usw.) überlesen.

Ein extremes Beispiel ist die "Fiathupe".
c'',e'' rein
c''e'' verstimmt
Hier sind tiefere Töne (sogenannte Differenztöne) hervorgehoben, die man nur sehr leise bei einem Zweiklang mithört.
(Die Verstimmung bei c'' e'' ist übrigens die der gleichstufigen Stimmung).

Frequenzverhältnisse gibt man mit möglichst kleinen Zahlen an:
c' hat die Frequenz von 264 Hz,
d' hat die Frequenz von 297 Hz,
,e' hat die Frequenz von 330 Hz,
g' hat die Frequenz von 396 Hz und
c'' hat die Frequenz von 528 Hz,
Also hat die Oktav c' c'' das Frequenzverhältnis c''/c' = 528/264 = 2/1
Entsprechend: Quinte c' g': 396/264 = 3/2
Quarte g' c'': 528/396 = 4/3
große Terz c' ,e': 330/264 = 5/4
kleine Terz ,e' g': 396/330 = 6/5
Sekunde: c' d': 297/264 = 9/8

Das Frequenzverhältnis ist unabhängig vom Grundton, entscheidend ist nur das Intervall..
Zum Beispiel ist:
das Frequenzverhältnis der Oktav von g' zu g'' = 792 : 396 = 2:1 und
das Frequenzverhältnis der Quint von g' zu d'' = 594 : 396 = 3:2.

Sie sehen hier auch - da das Frequenzverhältnis der Oktav 2:1 ist -, dass der Ton, der eine Oktav höher erklingt, doppelte Frequenz hat.

(Die Frequenz von g'' ist die doppelte von g', die von d'' die doppelte von d'.)

Die Frequenzverhältnisse aller Intervalle

(In Klammer stehen die künftig verwendeten Abkürzungen der Intervalle.)

Die Oktave (Ok): Frequenzverhältnis
Beispiel: c'' : c' = 528 Hz : 264 Hz = 2 : 1

Die Quinte (Qui): Frequenzverhältnis 3:2
Beispiel: g' : c' = 396 Hz : 264 Hz = 3 : 2

Die Quarte (Qua): Frequenzverhältnis 4:3
Beispiel: f' : c' = 352 Hz : 264 Hz = 4 : 3

Die Quinte und die Quarte ergänzen sich zur Oktave: Qui + Qua = Ok

Die große Terz (gT): Frequenzverhältnis 5:4 .
Beispiel: ,e' : c' = 330 Hz : 264 Hz = 5 : 4

Die kleine Sext (kSext): Frequenzverhältnis 8:5 .
Beispiel: 'as' : c' = 422,4 Hz : 264 Hz = 8 : 5

Die große Terz und die kleine Sext ergänzen sich zur Oktave: gT + kSext = Ok

Die kleine Terz (kT): Frequenzverhältnis 6:5 .
Beispiel: 'es' : c' = 316,8 Hz : 264 Hz = 6 : 5

Die große Sext (gSext): Frequenzverhältnis 5:3 .
Beispiel: ,a' : c' = 440 Hz : 264 Hz = 5 : 3

Die große Terz und die kleine Sext ergänzen sich zur Oktave: kT + gSext = Ok

Achtung: Es gibt zwei Ganztöne (Ganzton = Sekunde). Das ist der Grund, weshalb wir zwischen reiner, mitteltöniger, wohltemperierter und gleichförmiger Stimmung unterscheiden müssen. Am natürlichsten ist die reine Stimmung (das "diatonische Stimmungsprinzip" unserer Tonleitern), die wir hier zunächst besprechen. Da dies zu Schwierigkeiten bei Tasteninstrumenten bei Modulationen führt, hat sich heutzutage die gleichstufige Stimmung durchgesetzt, bei der zwölf Quinten sieben Oktaven ergeben und zwei Ganztöne eine große Terz.

Der große Ganzton (G): Frequenzverhältnis 9:8
Beispiel: d' : c' = 297 Hz : 264 Hz = 9 : 8
Der kleine Ganzton (G-): Frequenzverhältnis 10:9
Beispiel: ,e' : d' = 330 Hz : 297 Hz = 10 : 9

Entsprechend gibt es zwei kleine Septimen (kSept und kSept+).

Die kleine Septime kSept: Frequenzverhältnis 16:9
Beispiel: c'' : d' = 528 Hz : 297 Hz = 16 : 9

Die kleine Septime kSept+: Frequenzverhältnis 9:5
Beispiel: d'' : ,e' = 594 Hz : 330 Hz = 9 : 5

Der große Ganzton und der kleine Ganzton ergeben zusammen eine große Terz: G + (G-) = gT.

Ganzton und die kleine Septime ergänzen sich zur Oktave: G + kSept = Ok bzw. (G-) + (kSept+) = Ok

Der Halbton (H): Frequenzverhältnis 16:15.
Beispiel: f' : ,e' = 352 Hz : 330 Hz = 16 : 15

Die große Septime (gSept): Frequenzverhältnis 15:8.
Beispiel: ,h' : c' = 495 Hz : 264 Hz = 15 : 8

Halbton und die große Septime ergänzen sich zur Oktave: H + gSept = Ok

Bemerkung: Der geniale Pythagoras kam auf dieselben Verhältnisse über das Messen von Saitenlängen am Monochord.

Der geordnete additive Intervallraum

Je zwei Tönen x und y (mit den Frequenzen f1 und f2) ist eindeutig ein Intervall xy zugeordnet (mit dem Frequenzverhältnis q = f2:f1).
Beispiel: Die Oktave c'c'' hat das Frequenzverhältnis 528/264 = 2, die Reine reine Quinte c'g' das Frequenzverhältnis 396/264 = 3/2, die große Terz c',e' das Frequenzverhältnis 330/264 = 5/4 und die kleine Terz ,e'g' das Frequenzverhältnis 396/330 = 6/5.
Bemerkung: Euklid rechnete mit Proportionen, nämlich mit Saitenverhältnissen, die dem Kehrwert der Frequenzverhältnisse entsprechen.
Zu jedem Anfangston x (mit der Frequenz f1) und zu jedem Intervall i (mit dem Frequenzverhältnis q) ist eindeutig ein Endton y (mit der Frequenz f2 = f1·q) des Intervalls i = xy zugeordnet.
Beispiel: Hat ,a' hat die Frequenz f1 = 440 Hz, so hat der Ton c'', der um eine kleine Terz mit dem Frequenzverhältnis q = 6/5 höher erklingt, die Frequenz f2 = 440 Hz·6/5 = 528 Hz.
In der Sprache der Musiker werden Intervalle bei der Hintereinanderausführung addiert. Der Intervallraum besitzt in diesem Sinne eine additive Struktur.
Beispiel: große Terz + kleine Terz = Quinte.
12 Quinten sind ungefähr gleich wie 7 Oktaven. Der Unterschied wird als pythagoreisches Komma bezeichnet. Man schreibt dazu: pythagoreisches Komma = 12 Quinten - 7 Oktaven
Führt man drei reine große Terzen hinter einander aus (Zum Beispiel c - e - gis - his), so erhält man (von c nach his) ein Intervall, das etwas kleiner als die Oktave ist. Der Unterschied heißt kleine Diesis. Somit: kleine Diesis = Oktave - 3·(große Terz).
Der Addition von Intervallen entspricht die Multiplikation der Frequenzverhältnisse und der Subtraktion von Intervallen die Division der Frequenzverhältnisse.
Beispiel: Der Addition kleine Terz + große Terz = Quinte entspricht die Multiplikation 6/5· 5/4 = 3/2.
Das Frequenzverhältnis des pythagoreischen Kommas errechnet sich zu (3/2)12:27 = 531441/524288 und das der kleinen Dieses zu 2:(5/4)3 = 128/125.
Intervalle kann man in der Größe vergleichen: Dabei gilt: Je größer das Intervall, um so größer ist sein Frequenzverhältnis.
Das Frequenzverhältnis wächst exponentiell an.
Beispiel:
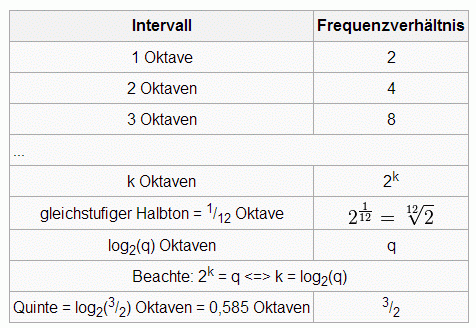
Tabelle
Intervalle kann man als Vielfache von einer Oktave angeben. Es handelt sich dabei um ein logarithmisches Maß der Frequenzverhältnisse. Mit der Untereinheit Cent mit der Definition 1200 Cent = 1 Oktave (oder 1 gleichstufiger Halbton= 100 Cent) wird ein sehr genauen Vergleich der Intervallgröße in ganzen Zahlen ermöglicht. Dieses Oktav- oder Centmaß ist dann proportional zur Intervallgröße.
Beispiel:
Tabelle log2(x)=log(x):log(2) (log = Lorarithmus zur Basis 10, log2 = Logarithmus zur Basis 2).
Durch die Verwendung des Logarithmus bei der Centberechnung wird aus der multiplikativen Struktur der Frequenzverhältnisse wieder die additive Struktur der Intervalle.
Beispiel:
Quinte = kleine Terz + große Terz = 315,641 Cent + 386,314 Cent = 701,955 Cent.
pythagoreisches Komma= 12·Quinte - 7·(Oktave) = 12· 701,955 Cent -7·1200 Cent = 23,460 Cent.
kleine Diesis= Oktave - 3·(große Terz) = 1200 Cent - 3·386,3137 Cent = 41,059 Cent (gerundet).
Mathematisch gesehen sind die im Folgenden beschriebenen Intervallräume archimedisch geordnete kommutative Gruppen.
Außer Tonhöhe und Lautstärke ist ein wichtiges Charakteristikum eines Tones die Klangfarbe.

Diese hängt davon ab, in wie stark die Obertöne mitschwingen. Man sieht dieses an der Schwingungsform.

Einen Ton, bei dem keine Obertöne mitschwingen, nennt man eine reine Sinusschwingung. Er klingt langweilig.
schwingung
Ton a' (reiner Sinuston)
Eine ganz andere Schwingungsform hat ein Ton, bei dem viele Obertöne mitschwingen. Hier:
Grundton:
    (440 Hz) 100%,
1 Oberton (Ok)
    (880 Hz) 25%
2. Oberton (Ok+Qui)
    (1320 Hz) 25%
3. Oberton (2Ok)
    (1760 Hz) 25%
4. Oberton (2Ok +gT)
    (2 200 Hz)100%( !)
Je mehr und stärker hohe Obertöne beigemischt sind, desto schärfer klingt der Ton.
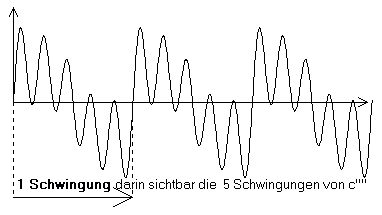
a1mitobertoenen
Ton a' (obertonreich)
Wenn Sie genau hinhören, können Sie die hohe Terz cis'''' in diesem Ton mithören.
cis'''

Die Analyse von Einzeltönen berüchsichtigt außer der Klangfarbe des ausgehaltenen Tones (sustain) auch den Einschwingvorgang (attack) und das Ausklingen (Release).

Die Obertöne eines Einzeltones können mehr oder weniger durch physikalische Eigenschaften des Klangkörpers abweichen. Bei tiefen Klaviertönen macht sich zum Beispiel die Steifigkeit der Saiten bemerkbar.

Körper, in denen sich die Schwingungen in mehrere Richtungen ausbreiten, wie zum Beispiel Röhren, Stäben, Platten oder Glocken, erzeugen oft keinen Einzelton sondern mehrere Töne mit ihren entsprechenden Obertönen, wobei diese dort häufig mehr oder weniger stark von den theoretischen Werten abweichen können.
Mit dem Programm TTmusik können bei Tönen und Akkorde angeben, welche Obertöne in beliebiger Stärke dem Sinuston beigemischt werden.

Weiter mit ...