Joachim Mohr Mathematik Musik Delphi
Lektionen
|
Lektionen der Vektorrechnung in
Aufgaben Lösungen |

|
Lösungen der 1. Lektion
Es ist hier unerheblich, wie Vektoren definiert werden.Vektor = Klasse von gleichlangen und gleichgerichteten Pfeilen oder
Vektor = Parallelverschiebung.
Häufig werden Pfeile (Repräsentanten von Vektoren) und Vektoren identifiziert. Dann gilt:
Vektoren darf man parallel verschieben.
Hinweis: Bis auf wenige Ausnahmen sind alle Figuren Planfiguren.
Diese veranschaulichen den Sachverhalt meist besser als maßstabsgerechte Zeichnungen.
Lösung der Vorübung: Gegenvektor, Addition und Subtraktion von Vektoren
-> -> ->
Hier sind a , b und c nicht die Ortsvektoren von A,B,C!
Achte stets auf das richtiges Vorzeichen!
Verwechse nie Anfangs- und Endpunkt eines Vektors.
Statt "drücke aus" sagt man mathematisch "Stelle als
Linearkombination" dar.
——> -> ——> ->
a) AB = a BA = - a .
-> ->
- a heißt der Gegenvektor von a .
——> -> -> -> -> ->
b) AC = a + b , c = a + b
——> -> -> -> -> -> -> ->
c) AB = c + (- b ) = c - b , a = c - b
——> -> -> -> -> -> -> ->
d) BC = - a + c = c - a , b = c - a .
|
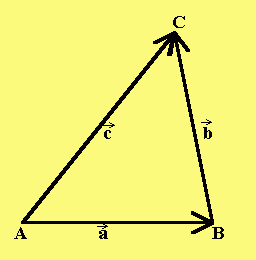
|
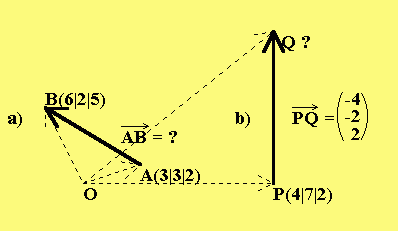
Lösung der 1. Aufgabe:
a) Einen Vektor berechnet man aus zwei Punkten durch Subtraktion (zweiter Punkt "-" erster Punkt.).b) Den Endpunkt des Vektors, der an einem Punkt angesetzt wird, erhält man durch Addition (Punkt "+" Vektor.)
Da man Punkte nicht addieren oder subtrahieren kann, muss man beim Berechnen auf die "Ortsvektoren" ausweichen. Die Rechnung ist allerdings genau dieselbe.
Beispiel:
——> ——> ——> ——> ——>
a) AB = -OA + OB = OB - OA
|6| |3| | 3|
——> | | | | | |
kurz AB = |2| - |3| = |-1|
| | | | | |
|5| |2| | 3|
|4| |-4|
——> ——> ——> | | | |
b) OQ = OP + PQ = |7| + |-2|
| | | |
|2| | 2|
kurz Q(4-4|7-2|2+2) = Q(0|5|4)
|
|
| Tipp: |
Zeichne möglichst keine Ortsvektoren mehr ein! Deine Planfiguren werden dadurch übersichtlicher. Merke Dir einfach diese zwei Regeln. |
Lösung der 2. Aufgabe:
|-2|
——> ——> | |
a) AD = BC = | 3| (Subtraktion) => D(6|3|7) (Addition).
| |
| 5|
——> -> -> -> -> ——> ——> -> ->
Subtraktion BC = c - b . Addition d = a + AD , da AD = d - a .
Hinweis: Ärgerlich ist, dass man Punkte nicht addieren
kann. Man weicht dann auf "Ortsvektoren" aus.
->
Der Ortsvektor a vom Punkt A hat dieselben Koordinaten.
| 1 |
——> | | ——>
b) M(5|4,5|4,5) BM = |-1,5| = MD
| |
| 2,5|
——> ——> ——> -> 1 ->
c) BM = BA + AM = - u + - v
2
d) S(0|0|7)
|
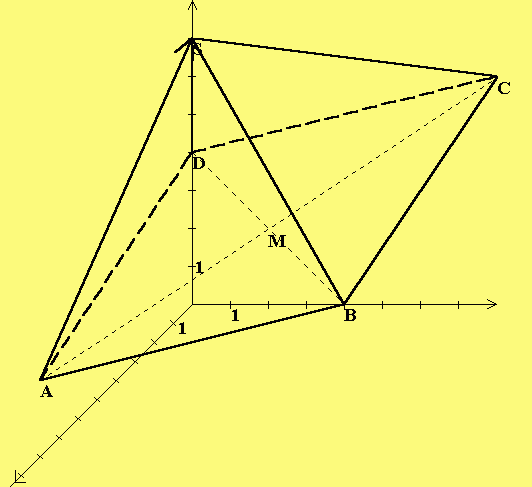
|
Lösungen der 2. Lektion
Lösung der Vorübung:
Lösung der 1. Aufgabe:
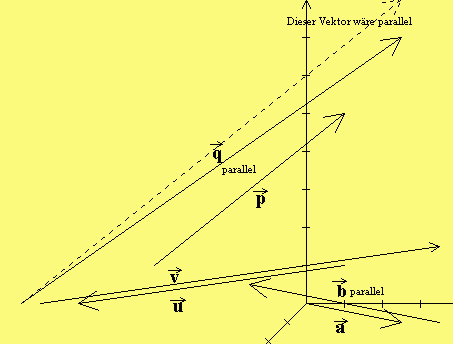
Zwei Vektoren sind linear abhängig, wenn ein Vektor ein Vielfaches des anderen Vektors ist.Repräsentanten (die Pfeile) sind dann parallel.
Ist der Nullvektor unter den beiden Vektoren, so sind sie linear abhängig.
|-1| | 2|
-> | | -> | | Linear abhängig
a) a = | 2| b = |-4|
| | | | -> ->
|-1| | 2| b = -2·a
| 6| |-9| Linear abhängig
-> | | -> | |
b) u = |-4| v = | 6| -> 3 ->
| | | | v = - -·u
| 2| |-3| 2
Oder: Man sieht sofort: Beide Vektoren sind
| 3|
| |
ein Vielfaches des Vektors |-2|.
| |
| 1|
|4| |8| Linear unabhängig. Wäre
-> | | -> | |
c) p = |3| q = |6| der zweite das Doppelte
| | | |
|2| |3| des ersten, müsste seine
3. Koordinate 4 sein.
Formal gerechnet: Der Ansatz
|8 = 4k|
-> -> | |
q = k·p führt auf das LGS |6 = 3k|,
| |
|3 = 2k|
der keine Lösung hat (Es kann nicht gleichzeitig
k =2 und k = 1,5 sein.
|
|
Lösung der 2. Aufgabe:
-> -> ->
Drei Vektoren a , b und c sind linear unabhängig, wenn die Gleichung
-> -> -> ->
xa + yb + zc = 0
nur die triviale Lösung x=0, y=0 und z=0 hat.
| 0| |1| | 2|
-> | | -> | | -> | |
a) a = |-6| b = |1| c = |-4|
| | | | | |
| 0| |1| | 2|
| y + 2z = 0| (1)
| |
Hier hat man das LGS zu lösen | -6x + y - 4z = 0| (2).
| |
| y + 2z = 0| (3)
| y + 2z = 0| (1)
| |
Dieses LGS ist äquivalent zu |-6x + y - 4z = 0| (2)
| |
| 0 = 0| (1) - (3)
und hat folgende Lösung: z beliebig, y = - 2z und x = -z.
Zum Beispiel ist z = 1 y = -2 und x = -1 eine nicht triviale Lösung.
-> -> ->
Also sind die Vektoren a , b und c linear abhängig.
-> -> -> ->
Bemerkung: Die Gleichung -a - 2b + c = 0 kann zum Beispiel nach c
-> -> ->
aufgelöst werden: c = a + 2b .
Deshalb liest man öfters auch folgende Definition:
Drei Vektoren sind linear abhängig, wenn einer dieser Vektoren
als Linearkombination der übrigen dargestellt werden kann.
|1| |2| |0|
-> | | -> | | -> | | ->
Beim Beispiel a = |0|, b = |0| und c = |1| kann c allerdings
| | | | | |
|0| |0| |0|
-> ->
nicht als Linearkombination von a und b dargestellt werden, wohl
-> -> -> -> -> ->
aber b als Linearkombination von a und c : b = 2a + 0c . Auch
diese drei Vektoren sind linear abhängig:
-> -> -> ->
Die Gleichung xa + yb + zc = 0 hat die nicht triviale Lösung: x=2 y=-1 z=0.
| 0| |1| |1|
-> | | -> | | -> | |
b) u = |-1| v = |0| w = |1|
| | | | | |
| 2| |2| |1|
| y + z = 0| (1)
| |
Hier hat man das LGS zu lösen | -x + z = 0| (2).
| |
|2x + 2y + z = 0| (3)
| y + z = 0| (1) | y + z = 0|
| | | |
<=> |-x + z = 0| (2) <=> |-x + z = 0|
| | | |
|2x - z = 0| (3')=(3)-2(1) | z = 0| (3') + (2)
Dieses Gleichungssystem hat offensichtlich nur die triviale Lösung
x=0, y=0 und z=0. Die Vektoren sind also linear unabhängig.
Lösung der 3. Aufgabe:
Lösung der 4. Aufgabe:
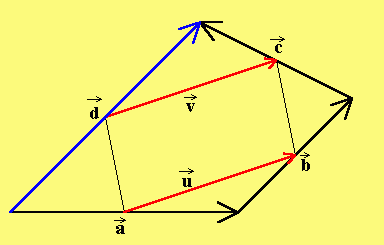
|
-> 1-> 1-> -> -> -> ->
a) u = -a + -b . Mit d = a + b + c folgt
2 2
-> 1-> 1-> 1 -> -> -> 1->
v = -d - -c = -(a + b + c ) - -c
2 2 2 2
1-> 1-> -> ->
= -a + -b . Man sieht u = v
2 2
-> ->
b) Mit u = v wurde gezeigt, dass bei dem
durch Verbinden der Seitenmitten
entstandenem Viereck zwei Gegenseiten
gleich lang und parallel sind.
Es ist somit ein Parallelogramm.
|
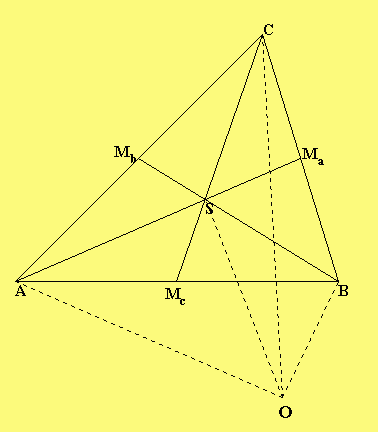
Lösungen der 3. Lektion
Lösung der 1. Aufgabe:
Lösung der 2. Aufgabe:
Es sind jeweils die Mittelwerte der Koordinaten zu berechnen.Bei den Seitenmitten das arithmetische Mittel von jeweils 2 Werten:
Ma(-2|-4|-3) Mb(-4|-2|1) und Mc(0|-1|-1).
Beim Schwerpunkt das arithmetische Mittel von jeweils 3 Werten:
S(-2|-7/3|-1)
Lösung der 4. Lektion I. Teil
Korrektur: Januar 2023| 1. Aufgabe: |
T teile die Strecke AB mit A(-12|3|-14) und B(9|-4|0) im Verhältnis 4:3.
Berechne die Koordinaten von T! |
——> 21 ——> 4——> 12
AB = (-7), AT = -AB = (-4) => T(0|-1|-6)
14 7 8
| 2. Aufgabe: |
Zeige T(-1|2|0) liegt auf der Strecke (AB) mit A(-6|7|-5) und B(2|-1|3).
In welchem Verhältnis teilt T die Strecke AB? |
Für A(-6|7|-5), T(-1|2|0) und B(2|-1|3) ist
| 5| | 3|
——> | | ——> | |
AT = |-5| und TB = |-3|.
| | | |
| 5| | 3|
Die Vektoren sind linear abhängig, also liegt T auf (AB).
——> ——>
Das Teilverhältnis k erkennt man sofort aus AT = k·TB zu k = 5:3.
Verallgemeinerung:
Oft betrachtet man das Verhältnis von AT zur ganzenStrecke AB. Dann gilt:
Oft betrachtet man das Verhältnis von AT zur ganzenStrecke AB. Dann gilt:
——> ——> ——> 1——>
Für die Mitte (Teilverhältnis 1:1) AT = TB => AT = -AB .
2
——> ——> ——> 2——>
Für den Schwerpunkt (Teilverhältnis 2:1) AT = 2TB => AT = -AB
3
——> x ——> ——> x ——>
Allgemein (Teilverhältnis x:y)AT = -·TB => AT = ———·AB
y x+y
——> 4——> ——> 4——>
Zum Beispiel: (Teilverhältnis 4:3) AT = -TB und AT = -BT
3 7
| | |
|——|——|——|——|——|——|——|
A 4 T 3 B
Lösung der 4. Lektion, II Teil
|
Lösung der 3. Aufgabe:
a) A(-1|1|-1) und M (2|-2|-4)
a
| 3| | 2|
——> | | ——> 2——> | |
=> AM = |-3| => AS = -AM = |-2|
a | | 3 a | |
|-3| |-2|
-> -> ——>
=> S(1|-1|-3) (Addition s = a + AS )
b) Mitte von A(-1|1|-1) und B(5|-3|-3) ist M (2|-1|-2)
c
|-1| |-3|
———> ———> | | | |
c) M C = 3·M S = 3·| 0| = | 0| => C(-1|-1|-5)
c c | | | |
|-1| |-3| -> -> ———>
(c = m + M C )
c c
|-3| |-6|
——> ——> | | | |
d) BC = 2·BM = 2·| 1| = | 2| => C(-1|-1|-5)
a | | | |
|-1| |-2| -> -> ——>
(c = b + BC )
|
4.Aufgabe:
a) T teilt A(-5|3|-9)B(2|-4|5) im Verhältnis 4:3.
| 7| | 4|
——> 4 ——> 4 | | | |
=> AT = -·AB = -·|-7| = |-4| => T(-1|-1|-1)
7 7 | | | |
|14| | 8|
|
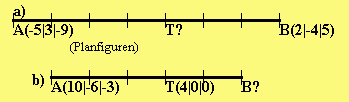
|
Lösungen der 5. Lektion
|
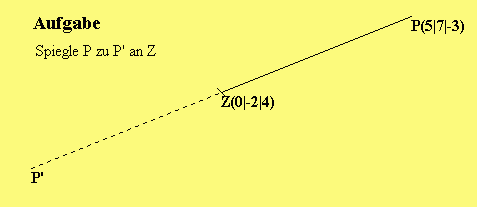
Lösung der 1. Aufgabe:
|-5|
——> ——> | |
ZP' = - ZP = |-9|
| |
| 7|
=> P'(-5|-11|11)
|
Lösung der 2. Aufgabe: Prinzipiell genügt es zwei Punkte der Gerade zu spiegeln und dann die Geradengleichung durch diese zwei Punkte anzuschreiben.
Rechnerische ein wenig einfacher, aber vor allem dem besseren Verständnis dienend, ist jedoch folgende Methode:
| 1| | 1|
-> | | | |
Um die Gerade g: x = |-2| + t·|-1| an Z(4|-3|2) zu spiegeln,
| | | |
| 3| | 0|
genügt es, den Aufpunkt P(1|-2|3) auf P'(7|-4|1) zu spiegeln (siehe Aufgabe 1).
Die Bildgerade g' ist dann parallel zu g. Somit:
| 7| | 1|
-> | | | |
g': x = |-4| + t·|-1|
| | | |
| 1| | 0|
Lösung der 3. Aufgabe: Prinzipiell genügt es
drei Punkte der Ebene zu spiegeln und dann die Ebenengleichung
durch diese drei Punkte anzuschreiben.Rechnerische wesentlich einfacher, aber vor allem dem besseren Verständnis dienend, ist jedoch folgende Methode:
Um die Ebene E: 2x1 + 3x2 - 2x3 = 4 an Z(0|3|-4) zu spiegeln, genügt es, einen Punkt P an Z auf P' zu spiegeln.
Die gesuchte Ebene E' ist dann die zu E parallele Ebene durch P'.
Zunächst bestimmen wir einen beliebigen Punkt auf E.
Vielleicht den Punkt, bei dem x1 = 0 und x2 = 0 ist.
Dann folgt aus der Ebenengleichung 2·0 + 3·0 -2x3 = 4.
Mit P(0|0|-2) haben wir also einen Punkt von E gefunden.
Der gespiegelte Punkt ist dann P'(0|6|-6) (siehe Aufgabe 1).
Die zu E parallele Ebene E' hat die Gleichung 2x1 + 3x2 - 2x3 = d.
Punktprobe mit P ergibt 2·0 + 3·6 -2·(-6) = 30 = d.
Somit: ist die gespiegelte Ebene E': 2x1 + 3x2 - 2x3 = 30
Lösungen der 11. Lektion
Lösung der 1. Aufgabe:
Aufgabe: Stelle die Gleichung (genauer die Parameterform) der Geraden gdurch A(-4|1|3)und B(2|-1|2) und prüfe, ob der Punkt P(-10|3|4) oder der Punkt Q(-10|3|3) auf g liegt.
Lösung: Als "Aufpunkt" ("Stützvektor") wählen wir A ("den Ortsvektor von A").
——>
Als "Richtungsvektor" den Vektor AB .
|-4| | 6|
-> | | | |
g: x = | 1| + t·|-2|
| | | |
| 3| |-1|
Um zu prüfen, ob die Punkte P und Q auf g liegen, machen wird die Punktprobe.
|-10| |-4| | 6| |-10| |-4| | 6|
| | | | | | | | | | | |
für P: | 3 |= | 1| + t·|-2| für Q: | 3 |= | 1| + t·|-2|
| | | | | | | | | | | |
| 4 | | 3| |-1| | 3 | | 3| |-1|
Für P gibt es ein passendes t, nämlich t = -1, für Q nicht. Somit:
P liegt auf g, Q liegt nicht auf g.
Lösung der 2. Aufgabe:
|-4| | 6| |-10| |-12|
-> | | | | -> | | | |
g: x = | 1| + t·|-2| und h: x = | 3 | + t·| 4 |
| | | | | | | |
| 3| |-1| | 4 | | 2 |
-> ->
P u Q v
(Die Aufpunkte und Richtungsvektoren)
-> ->
a) g und h sind parallel, da die Richtungsvektoren u und v linear abhängig sind.
b) Wir prüfen, ob der Aufpunkt Q von h auf g liegt. Punktprobe
|-10| |-4| | 6|
| | | | | |
für Q: | 3 |= | 1| + t·|-2| liefert passendes t = -1 (Probe stimmt!)
| | | | | |
| 4 | | 3| |-1|
Q liegt also auf g und somit sind beide Geraden identisch.
Lösung der 3. Aufgabe:
a) Die Geraden sind offensichtlich nicht parallel. Wir Prüfen, ob sie sich schneiden:
Gleichsetzen der Gleichungen mit verschiedenen Parametern s und t ergibt:
|1| | 2| |-2| | 1|
| | | | | | | |
|1| + s | 1| = | 2| + t |-2| mit der Lösung s = - 1 und t = 1
| | | | | | | |
|0| |-2| | 0| | 2|
Ergebnis: Die Geraden schneiden sich in S(-1|0|2) (Probe stimmt!)
b) Die Gleichungen der Geraden sind
| 1| |1| |1| |-2|
-> | | | | -> | | | |
g: x = | 0| + s |2| und h: x = |2| + t |-4|
| | | | | | | |
|-1| |2| |3| |-6|
oder besser
| 1| |1| |1|
-> | | | | -> | |
g: x = | 0| + s |2| und h: x = t|2|
| | | | | |
|-1| |2| |3|
Sie sind offensichtlich nicht parallel. Die Prüfung, ob sie einen
Schnittpunkt haben, führt zu einem Widerspruch (Probe stimmt nicht!).
Ergebnis: Die Geraden sind windschief.
Lösung der 21. Lektion
Vektorgleichung LGS
|x | |4| |-3| |-5| x = 4 - 3s - 5 t
| 1| | | | | | | 1
a) E: |x | = |2| + s|-1| + t|-4| x = 2 - s - 4t
| 2| | | | | | | 2
|x | |3| | 2| | 1| x = 3 + 2s + t
| 3| 3
Elimination von s und t führt auf die Koordinatengleichung von E.
Zunächst: zwei Gleichungen ohne t:
x + 5x = 19 + 7s x + 4x = 14 + 7s
1 3 2 3
Nun eine Gleichung ohne t und s ergibt die Koordinatengleichung von E.
(x + 5x ) - (x + 4x )= 19 - 14
1 3 2 3
Somit: E: x - x + x = 5
1 2 3
Zweiter Lösungsweg:
Mit Hilfe des Vektorproduktes kann man |-3| |-5| | | | | aus den Richtungsvektoren |-1| und |-4| der Ebene E: ax + bx + cx = d | | 1 2 3 | 2| | 1| |a| |-3| |-5| | -1 + 8| | 7| | | | | | | | | | | sofort berechnen: |b| = |-1|x|-4| = |-10 + 3| = |-7|. | | | | | | | | | | |c| | 2| | 1| | 12 - 5| | 7| Die Ebene hat also die Gleichung: 7x - 7x + 7x = d. 1 2 3 Punktprobe mit dem Aufpunkt P(4|2|3) ergibt 7·4 - 7·2 + 7·3 = 35 = d. Somit E: 7x - 7x + 7x = 35 oder (besser) E: x - x + x = 5. 1 2 3 1 2 3 b) Für die Ebene durch A(-1|3|-4) B(2|-5|3) und C(1|-3|2) stellen wir zunächst die Parameterform auf: |-1| | 3| | 2| -> | | | | | | E: x = | 3| + s|-8| + t|-6| | | | | | | |-4| | 7| | 6| ——> ——> A AB AC (Aufpunkt und Richtungsvektoren von E) Lösung mit Hilfe der Elimination von s und t (oder mit Hilfe des Vektorproduktes): E: 3x + 2x + x = -1 1 2 3Hinweis: Da man Ebenen besser immer in Koordinatenform verwendet, berechnet TTMathe die Ebenengleichung.
Lösung der 22. Lektion
a) Gesucht: Schnittpunkt der Ebene E mit der Geraden g
| 3| | 3|
-> | | | |
E: 2x + 4x + 3x = 1 g: x = |-1| + t·|-1|
1 2 3 | | | |
|-1| |-1|
Gesucht wird also der Punkt, der gleichzeitig auf E liegt, also
die Gleichung von E erfüllt, und auf g liegt, zu dem also ein
passendes t existiert. Dies finden wir, indem wir
x = 3 + 3t, x = -1 - t und x = -1 -t in E: 2x + 4x + 3x = 1 einsetzen.
1 2 3 1 2 2
Dies ergibt 2(3 + 3t) + 4(-1 - t) + 3(-1 - t) = 1 => - t - 1 = 1. Somit t = - 2.
Dieses t in die Parametergleichung von g eingesetzt ergibt den Schnittpunkt S(-3|1|1).
b) Dass E parallel zur x -Achse verläuft, erkennt man folgendermaßen:
2
Betrachte einen beliebigen Punkt X(x |x |x ) auf E (er erfüllt die Gleichung von E)
1 2 3
und verschiebe ihn in Richtung x -Achse zu X(x |x + 1|x ). Dann erfüllt er immer
2 1 2 3
noch die Gleichung der Ebene E (da x nicht vorkommt).
2
Somit: Ebene E und Gerade g verlaufen parallel: Kein Schnittpunkt.
Alternative Lösung:
Wie in a) gerechnet erhält man, um den Parameter t zu ermitteln: 0 - 4·0 = 10,
also einen Widerspruch. Die Annahme, ein passendes t existiere, ist also falsch.
(Hätte man die Gleichung 0 = 0 erhalten, läge g ganz in E).
c) 1. Lösung: Wir schreiben E: 2x - 4x + 3x = - 2 (siehe Lektion 21)
1 2 3
und rechnen wie in Teil a). Ergebnis: s = 1 Schnittpunkt S(5|3|0)
2. Lösung (nicht empfehlenswert, da bei allen weiterführenden Aufgaben sowieso
die Koordinatengleichung von E benötigt wird).
Parametergleichung von g (mit dem Parameter r(!)) und Parametergleichung
von E (mit Parametern s und t) gleichsetzten. Ergibt ein LGS mit der Lösung:
r = 1, s= - 1 und t = 1. Also Schnittpunkt S(5|3|0)
Lösung der 23. Lektion
Schnittgerade zweier Ebenen
Sind die beiden Ebenen in Koordinatenform gegeben (und dafür werden wir stets sorgen), dann sind alle Punkte gesucht, welche die beiden Ebenengleichungen erfüllen. Wir müssen also ein lineares Gleichungssystem mit zwei Gleichungen und drei Unbekannten lösen. Im allgemeinen Fall gibt es dann unendlich viele Lösungen, die wir mit Hilfe eines Parameters t darstellen können. Wir erhalten dadurch die Parameterform der Geradengleichung.
a) E : 2x + 11x + 4x = 1 (1) E : x + 6x + x = 4 (2)
1 1 2 3 2 1 2 3
Wir suchen also die Lösungsmenge der Gleichungen (1) und (2).
|2x + 11x + 4x = 1| (1)
Eine einfache Äquivalenzumformung ergibt: | 1 2 3 |
| |
| x - 2x = 7| 2·(2) - (1)
2 3 |
Wir können eine Variable frei wählen. Zum Beispiel x = t.
3
Dann ergibt sich: x = 7 + 2t und x = -38 - 13t.
2 1
|-38| |-13|
-> | | | |
Somit: Schnittgerade g: x = | 7 | + t| 2 |.
| | | |
| 0 | | 1 |
Der Aufpunkt der Geraden ist hier P(-38|7|0) er könnte auch sein P(1|1|-3) (mit t=-3 gerechnet) usw.
Falls Du eine andere Lösung erhalten hast, kann die anders aussehen. Auf jeden Fall:
|-13|
| |
Dein Richtungsvektor ein Vielfaches von | 2 | sein und Dein Aufpunkt beide Ebenengleichungen erfüllen.
| |
| 1 |
Mit Hilfe des Vektorproduktes kannst Du Deine
Löung überprüfen:Der Richtungsvektor der Schnittgeraden muss ein Vielfaches des Vektorproduktes der Normalenvektoren sein, da der Richtungsvektor auf beiden Normalenvektoren senkrecht steht.
| 2| |1| |11 - 24| |-13|
| | | | | | | |
Probe: |11| x |6| = | 4 - 2| =| 2| stimmt!
| | | | | | | |
| 4| |1| |12 - 11| | 1|
b) Man erkennt auch sofort, dass die Normalenvektoren der
Ebenen linear abhängig sind.Die Ebenen sind also parallel oder identisch.
Die Lösungsmenge des zugehörigen LGS ist leer. Die beiden Ebenen haben also keine gemeinsamen Punkte.
Die Ebenen sind parallel.
c) Wir ermitteln zunächst die Koordinatengleichungen (Lektion 21).
E : -2x + 11*x + 5*x = 23 (1) E : - x + 2x + 3x = -8 (2)
1 1 2 3 2 1 2 3
mit der Zwischenrechnung (1) - 2(2): 7x - x = 39 setzen wir x = t
2 3 2
und erhalten x = - 39 + 7t und x = - 109 + 23t.
3 1
|-109| |23|
-> | | | |
Somit: Schnittgerade g: x = | 0 | + t| 1| oder mit einfacheren Aufpunkt (t = 5)
| | | |
| -39| | 7|
| 6| |23|
-> | | | |
g: x = | 5| + t| 1|.
| | | |
|-4| | 7|
Lösung der 24. Lektion
a) E: 2x + 3x + 4x = 12
1 2 3
Schnittpunkt mit der x -Achse erhält man durch x = 0 x = 0 => A(6|0|0)
1 2 3
Schnittpunkt mit der x -Achse erhält man durch x = 0 x = 0 => B(0|4|0)
2 1 3
Schnittpunkt mit der x -Achse erhält man durch x = 0 x = 0 => C(0|0|3)
3 1 2
|6| |-3| |0| | 0|
-> | | | | -> | | | |
Spurgeraden: (AB): x = |0| + s·| 2| (BC): x = |4| + s·|-4| und
| | | | | | | |
|0| | 0| |0| | 3|
|6| |-2|
-> | | | |
(AC): x = |0| + s·| 0|
| | | |
|0| | 1|
b) E: -2x + 3x + 4x = 12. Spurpunkte A(-6|0|0) B(0|4|0) C(0|0|3)
1 2 3
Spurgeraden wie in a), jedoch statt 6 bzw. - 6 nun -6 bzw. 6.
| a) |
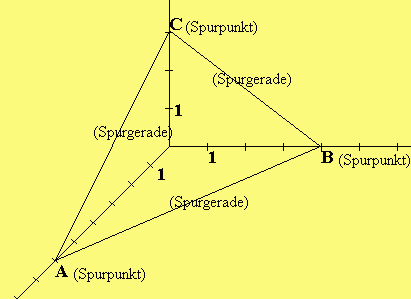
|
b) |
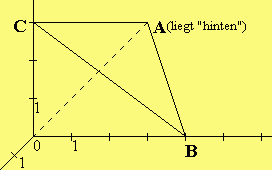
|
Lösung der 25. Lektion
25. Lektion: Abstand paralleler Ebenen
Aufgabe: Zeige, dass die Ebenen parallel sind und berechne ihren Abstand.
a)
E : 2x -3x + x =14
1 1 2 3
E : 2x -3x + x =42
2 1 2 3
Lösungen
a) Die Ebenen sind parallel, da die Normalenvektoren die gleiche Richung haben.
→ 2
Wir schneiden mit der senkrechten Geraden x = t(-3) die Gerade E und
1 1
erhalten mit t=1 den Schnittpunkt P (2|-3|1) und die Gerade E und
1 2
erhalten mit t=3 den Schnittpunkt P (6|-9|3). Der Abstand der beiden
2
———→ ——————— ——
Ebenen ist dann |P P | = √16+36+4 = 2√14
1 2
2. Lösung mit Hilfe der Hesseschen Normalenform:
Wir setzten bei der Ebene E x =0 und x =0 ⇒x =7. Also ist P(7|0|0) ein Punkte der Ebene E .
1 2 3 1 1
2x -3x + x -42
1 2 3
Die Hessesche Normalenform von E ist ——————————————— = 0
2 √4+9+1
Der Abstand d der beiden Ebenen ist gleich dem Abstand des Punktes P(7|0|0) von E , also
2
14-42 ——
d=|—————| = 2√14.
√4+9+1
→ 4 -3 -5
b) E: x = ( 2) +u(-1)+v(-4)
1 3 2 1
E : x - x + x = 10
2 1 2 3
Lösung:
Wir wandeln zunächst E um in Parameterform:
1
E : x - x + x = 5
1 1 2 3
→ 1
Wir schneiden mit der senkrechten Geraden x = t(-1) die Gerade E in P und E in Q.
1 1 2
5 5 5 10 10 10 —→ 5
P(—|-—|—) Q(——|-——|——) Abstand |PQ| =— √3
3 3 3 3 3 3 3
2.Lösung für b)
Wir berechnen mit Hilfe des Vektorprodukts den Normalenvektor von E :
1
3 -5 7 1
(-1)×(-4)=( 7) hat die gleiche Richung wie der Normalenvektor (-1)
2 1 -7 1
von E . Also sind E und E parallel.
2 1 2
x - x + x - 10
1 2 3
Wir berechnen mit der Hesseschen Normalenform von E ———————————————— = 0
2 √3
4-2+3-10 5
den Abstand d von P(4|2|3) von E : d=|————————| = —√3
2 √3 3
Lösung der 31. Lektion
Lösung der Vorübung:
|a | —————————
-> | 1| /2 2 2
a) Allgemein a = |a | = ||a || = \/a + a + a
| 2| 1 2 3
|a |
| 3|
| 5|
-> | | ——————————— —— -
Hier: a = |a | = ||-4|| = \/25 + 16 + 9 = \/50 = 5\/2
| |
| 3|
—— ——>
b) Allgemein: d(P,Q) = PQ = |PQ |
| 2|
——> | | —— ——
Für P(4|-3|-6) und Q(6|5|-10) ist |PQ | = | 8| = \/84 = 2\/21
| |
|-4|
Bei den folgenden beiden Aussagen ist es gleichgültig,
ob man die erste als Definition des Skalarprodukts nimmt und die zweite beweist
oder umgekehrt.
-> -> -> ->
I a · b = |a |·|b |·cosα, wobei
α der von den Vektoren eingeschlossene Winkel ist.
|a | |b |
-> | 1| -> | 1| -> ->
II. Für a = |a | und b = |b | ist a ·b = a b + a b + a b
| 2| | 2| 1 1 2 2 3 3
|a | |b |
| 3| | 3|
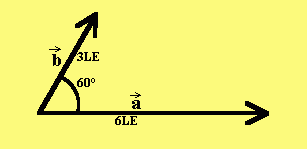
Lösung der Aufgabe:
-> -> a) a ·b = 6·3·cos60° = 9 Beim Kosinus: Taschenrechner
auf "deg" (Gradmaß) nicht rad (Bogenmaß). |-4| |-3| -> -> | | | | b) a ·b = | 7|·|-2| = (-4)·(-3) +7·(-2) + (-2)·(-5) = 8 | | | | |-2| |-5|
Lösung der 32. Lektion
Lösung der 1. Aufgabea) Zwei Vektoren stehen senkrecht aufeinender (sind orthogonal), wenn ihr Skalarprodukt Null ist.
|-3| | 4|
-> -> | | | |
a) a ·b = | 4|·|-3| = (-3)·4 + 4·(-3) + (-6)·(-4) = 0
| | | |
|-6| |-4|
Somit sind die Vektoren senkrecht aufeinander.
b) Zwei Geraden stehen senkrecht aufeinender (sind
orthogonal), wenn das Skalarprodukt ihrer Richtungsvektoren Null
ist.
| 3| | 3| | | | | | 1|·|-1| = 9 - 1 - 8 = 0. Die Geraden sind orthogonal. | | | | |-4| | 2| Schnittpunkt ist übrigens S(2|2|1) (Setze bei g s=-1)c) Zwei Ebenen stehen senkrecht aufeinender (sind orthogonal), wenn das Skalarprodukt ihrer Normalenvektoren Null ist.
E : 2x - 4x = 7 E : 8x + 11x + 4x = 0
1 1 3 2 1 2 3
Die Koordinaten der Normalenvektoren sind die Koeffizienten der Gleichung.
| 2| | 8|
| | | |
| 0|·|11| = 16 + 0 - 16 = 0. Die Ebenen sind orthogonal.
| | | |
|-4| | 4|
Lösung der 2. Aufgabe:Stell Dir vor: g paralle E oder g senkrecht zu E?
Welche Lage haben dann der Normalenvektor von E und der Richtungsvektor von g zueinender.
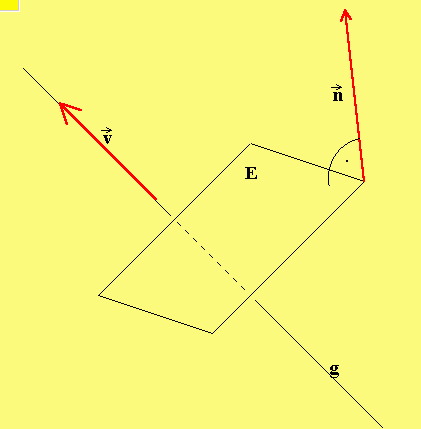
-> ->
Allgemein: Ist v der Richtungsvektor von g und n der Normalenvektor von E,
-> ->
dann gilt: g ist parallel zu E wenn v · n = 0 ist.
-> ->
Und: g ist senkrecht zu E wenn v und n linear abhängig sind.
|-3| | 3|
-> | | -> | |
Hier ist v = | 2| und n = |-2| .
| | | |
| 4| | 2|
-> ->
Es ist v · n = -9 -4 + 8 ≠ 0, also ist g nicht parallel zu E.
-> -> -> ->
n ist auch kein Vielfaches von v , also sind v und n linear unabhängig.
Folgerung: g schneidet E nicht rechtwinklig.
|a| | 2|
3. Ist n = |b| =|-5| und P(p |p |p ) = P(3|-7|11) ε E, dann kann man
|c| | 0| 1 2 2
die Ebenengleichung sofort folgendermaßen angeben:
|x - p | |a| |x - 3| | 2|
-> -> -> | 1 1| | | | 1 | | |
I E: (x - p )·n = 0 => E: |x - p |·|b| = 0 => E: |x + 7|·|-5| = 0
| 2 2| | | | 2 | | |
|x - p | |c| |x - 11| | 0|
| 3 3| | | | 3 | | |
=> E: 2(x -3) + (- 5)(x + 7) + 0(x - 11) = 0 => E: 2x - 5x = 41
1 2 3 1 2
->
II E: ax + bx + cx = d, wobei a,b,c durch n und d durch P bestimmt ist.
1 2 3
Also: E: 2x - 5x = d. Punktprobe mit P(3|-7|11) ergibt 2·3 - 5·(-7) = d
1 2
Somit E: 2x - 5x = 41.
1 2
-> | 0| | 2|
4. g: x = | 8| + t·| 0|
|-11| |-7|
5. E: -x + 2x = - 8
2 3
6.
| 1| | 2| |x - 1| | 2|
-> | | | | | 1 | | |
E: (x - |-2|)·|-6| = |x + 2|·|-6| = 2(x - 1) - 6(x + 2) + 3(x - 3) = 0
| | | | | 2 | | | 1 2 3
| 3| | 3| |x - 3| | 3|
| 3 | | |
=> E: 2x - 6x + 3x = 23.
1 2 3
Die Koordinatengleichung kann man auch als "Normalengleichung" betrachten.
Lösungen der 33. Lektion
(Hinweis: Die Lösungen wurden mit TTMathe gerechnet).Aufgabe 1:
—————
-> |a| /2 2 2
Der Betrag eines Vektors a = | | ist \/a + b (in R )
|b|
|a| —————————
-> | | /2 2 2 3
Der Betrag eines Vektors a = |b| ist \/a + b + c (in R )
| |
|c|
- —— ——
a) 5; 6,5; 5; \/5; 2\/10 b) 3; 7; 11; 13; \/14
Aufgabe 2:
-> ->
a · b
Für den Winkel α gilt: cosα = —————————
|->| |->|
|a |·|b |
33 3
a) cosa = ———— => a = 59,5° b) cosa = ————————— => a = 83,9°
5·13 —— ——
\/21·\/38
Aufgabe 3:
|-4| |4| | 8|
——> | | ——> | | ——> | | —— ——
AB = | 3| AC = |0| BC = |-3| a = \/82 b = 4 c = \/34
| | | | | |
| 3| |0| |-3|
α =133,3° β = 18,7° γ = 27,9°
Aufgabe 4:
a) Ein Schnittwinkel ist der Winkel, den die Richtungsvektoren einschließen,
(Der zweite Winkel dann der Ergänzungswinkel zu 180°.)
Dadurch, dass wir den Betrag verwenden, erhalten wir α ≤ 90°.
|-> ->|
|u · v |
Für den Winkel α gilt: cosα = ————————— für die
|->| |->|
|u |·|v |
|-2| | 9|
-> | | -> | |
Richtungsvektoren u = | 6| und v = |-6|.
| | | |
| 3| | 2|
48
cosα = ———— => α = 51,4°
7·11
b) Ein Schnittwinkel ist der Winkel, den die Normalenvektoren einschließen.
|-> ->|
|u · v |
Für den Winkel α gilt: cosα = ————————— für die
|->| |->|
|u |·|v |
| -3| | 2|
-> | | -> | |
Normalenvektoren u = | 4| und v = |14|.
| | | |
|-12| |-5|
110
cosα = ————— => α = 55,7°
13·15
c) Wir berechnen einen Winkel α' mit dem Richtungsvektor und Normalenvektoren.
Der gesuchte Schnittwinkel ist dann α =90° - α'.
|-> ->|
|u · n |
Für den Winkel α gilt: cosα' = sin α = —————————, da sin(90°-α') = cos α
|->| |->|
|u |·|n |
|-2| | 3|
-> | | -> | |
Richtungsvektor von g: u = | 6| Normalenvektor von E : v = | 4|
| | 1 | |
| 3| |-12|
18
=> sinα = ———— => α = 11,4°
7·13
Lösung der 34. Lektion
16.04.2008: Danke Georg für's Korrekturlesen!
a) gesucht Abstand des Punktes P(-1|2|1) von der Ebene E: 2*x - x - 5x = 3.
1 2 3
-> |-1| | 2|
I. Lösungsweg (ohne Formel): Die Gerade g: x = | 2| + t·|-1| durch P senkrecht zu E
| 1| |-5|
1 3
schneidet E im Punkt F(- -|1- |-1).
5 5
——> 2 ——
dann ist d(P,E) = |FP | = -\/30 = 2,191 LE.
5
II. Lösungsweg: Die Hesse-Form von E: ax + bx + cx - e = 0 ist
1 2 3
ax + bx + cx - e 2x - x - 5x - 3
1 2 3 1 2 3
———————————————— = 0. Hier ——————————————— = 0.
————————————— ——
/2 2 2 \/30
\/a + b + c
P(p |p |p ) = P(-1|2|1) hat dann von E den Abstand d = d(P,E)
1 2 3
| ap + bp + cp - d| | |
| 1 2 3 | |2·(-1) - 2 - 5 - 3| 12 2 ——
d = | ————————————————| Hier d= |——————————————————| = ———— = -\/30 LE
| ———————————— | | —— | —— 5
| /2 2 2 | | \/30 | \/30
|\/a + b + c |
(Kontrollrechnung mit TTMathe "Geometrie|Abstand Punkt Ebene")
Lösung der 35. Lektion
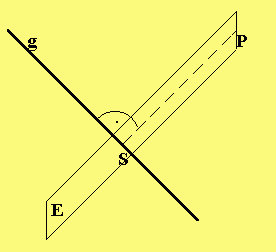
|
Bestimme zunächst eine Hilfsebene E durch P senkrecht zu g und dann den Schnittpunkt S von E mit g. Dann ist d(P,g) = d(P,S). |
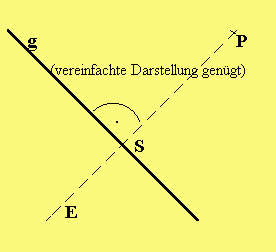
|
Rechnung:
|4| |1|
Gegeben g: x = |2| + t·|1| und P(4|6|2).
|1| |0|
Gesucht Abstand d = d(P,g). Wir berechnen zunächst mit
der Hilfsebe E: x + x = 10 durch P senkrecht zu g
1 2
den Schnittpunkt F von E mit g. Das führt zur
Gleichung (4+t) + (2 + t) = 10 mit der Lösung
——> |-2|
t = 2 und F(6|4|1) => d = |FP | = || 2|| = 3 LE
| 1|
Lösung der 36. Lektion
Gesucht: Der Abstand der windschiefen Geraden
-> |8| |3| -> | 7| |3|
g: x = |8| + s·|2| und h: x = | 2| + t·|3|
|5| |2| |10| |4|
-> |a| -> | |3| -> | |3|
1. Schritt: Suche Vektor n = |b| mit n ——— |2| und n ——— |3|.
|c| |2| |4|
3a + 2b + 2c = 0 3a + 2b + 2c = 0
( ) <=> ( )
3a + 3b + 4c = 0 b + 2c = 0
2 -> | 2|
Lösung: c beliebig, b = -2c, a = -c. Eine Lösung genügt. Zum Beispiel n =|-6|
3 | 3|
Mit Hilfe des Vektorproduktes kann man
-> -> |3| |3| |8 - 6| | 2|
n direkt berechnen: n = |2|x|3|= |6 - 12| = |-6|.
|2| |4| |9 - 6| | 3|
-> 1 -> 1| 2|
2. Schritt: Bilde den Einheitsvektor: n = ————n = -|-6| .
o |->| 7| 3|
|n |
-> -> -> 1|-1| | 2| 1
3. Schritt: Formel d(g,h) = |(q - p )·n | = -|-6|·|-6| = -(-2 + 36 + 15) = 7LE
0 7| 5| | 3| 7
Lösung der 37. Lektion
Lösung der Aufgabe: Gegeben ist die Ebene E:x1 - 2x2 + x3 = 7.
a) Um den Punkt P(5|-5|4) zu spiegeln,
bestimmen wird zunächst den Schnittpunkt F der
| 5| | 1|
-> | | | |
Geraden h: x = |-5| + t·|-2| durch P
| | | |
| 4| | 1|
senkrecht zu E mit E.
(5 + t) - 2(-5 - 2t) + (4 + t) = 7
=> t = -2 => F(3|-1|2).
|-2|
——> ——> | |
Aus FP' = - FP = | 4| folgt P'(1|3|0)
| |
|-2|
|
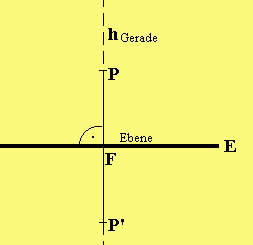
|
| 5| | 1|
-> | | | |
b) Um die Gerade g: x = |-5| + t| 1| zu spiegeln,
| | | |
| 4| |-5|
spiegeln wir die Punkte P(5|-5|4) zu P'(1|3|0)
und Q(6|-4|-1) (t=1 in g) zu Q'(4|0|-3).
|1| | 1|
——> -> | | | |
Somit g' = P'Q': x = |3| + t·|-1|
| | | |
|0| |-1|
Hinweis: Das Lot von P auf E schneidet E in F(3|-1|2),
das Lot von Q auf E in G(5|-2|-2).
——>
Den Vektor PF an F angesetzt ergibt P'(1|3|0),
——>
den Vektor QG an G angesetzt ergibt Q'(4|0|-3).
Der Aufpunkt von g' ist P'(1|3|0),
——> 1——>
der Richtungsvektor von g' ist P'Q' oder auch -P'Q'
3
|
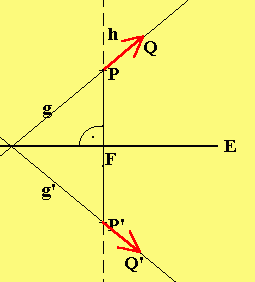
|
c) um die Ebene E*: x + x - 5x = 1 zu spiegeln,
1 2 3
spiegeln wir einen Punkt A(1|0|0) von E* zu A'(3|-4|2)
| 1|
->* | |
und B(2|1|-5) (an A Normalenvektor n = | 1| angesetzt)
| |
|-5|
| 3|
->*' ———> | |
zu B'(6|-7|-1) => n = A'B' = |-3|
| |
|-3|
Somit E*': x - x - x = 5.
1 2 3
|
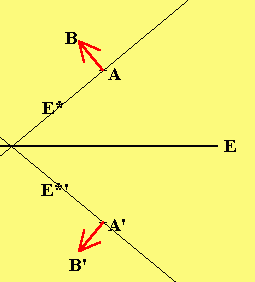
|
Lösung der 38. Lektion
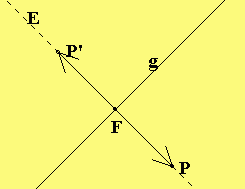
|
|1| |1|
-> | | | |
Um den Punkt P(1|8|4) an der Geraden x = |0| + t·|1|
| | | |
|0| |1|
zu spiegeln, bestimmen wir zunächst den Schnittpunkt F
der Ebene E: x + x + x = 13 durch P senkrecht zu g mit g.
1 2 3
(1+t) + t + t = 13 => t = 4 => F(5|4|4).
| 4|
——> ——> | |
Aus FP' = - FP = |-4| folgt P'(9|0|4)
| |
| 0|
|
39. Lösung der 39. Lektion
Aufgabe: Berechne mit Hilfe des Vektorprodukts den Flächeninhalt des DreiecksA(2|2|0)B(6|2|-1)C(2|3|-1)!
Zeichne das Dreieck in ein Koordinatensystem!
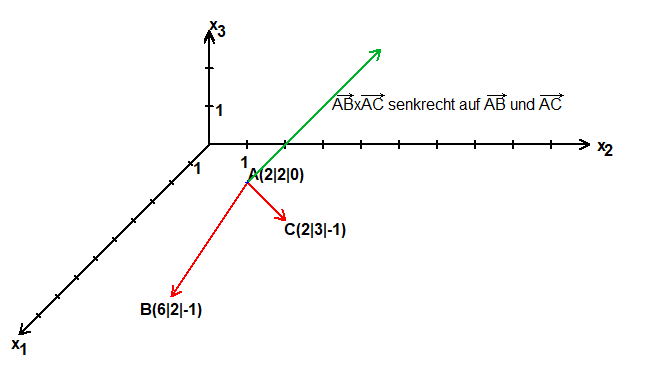
Zunächst wird das Vektorprodukt berechnet.
Sein Betrag ist der Flächeninhalt des Parallelogramms, das von
—→ 4 —→ 0
AB = ( 0) und AC = ( 1) aufgespannt wird:
-1 -1
—→ —→ 1
ABxAC =(4)
4
1 ——
Flächeninhalt des Dreiecks ABC=—√33 ≈ 2,872
2
Lösung der 41. Lektion
Lösung der Aufgabe:a)
|
| 2| |-2|
-> | | | |
Auf g: x = |-1| + t| 1| liegt P (2|-1|3)
| | | | 0
| 3| | 2|
->
Der Richtungsvektor v hat den Betrag 3.
Für die gesuchten Punkte P gilt:
1,2
|-2| |-10/3|
———> 5-> 5| | | |
P P = ± -v =±-| 1| = ±| 5/3|
0 1,2 3 3| | | |
| 2| | 10/3|
1 2 1 1 2 1
=> P (-1 -|- -|6 -) und P (5 -|-2 -|- -)
1 3 3 3 2 3 3 3
|
b)
|
Auf E: x - 2x + 2x = 5 liegt P (5|0|0) (x = 0, x = 0)
1 2 3 0 2 3
->
Der Normalenvektor n hat den Betrag 3.
Auf den parallele Ebenen liegen die Punkte P ,
1,2
| 1| | 5/3|
———> 5-> 5| | | |
für die gilt: P P = ± -v =±-|-2| = ±|-10/3|
0 1,2 3 3| | | |
| 2| | 10/3|
2 1 1 1 2 1
=> P (6-|- 3-|3 -) und P (3-|-3-|3-)
1 3 3 3 2 3 3 3
Die zu E parallelen Ebenen haben die Gleichung
E: x - 2x + 2x = d . Punktprobe mit P und P ergibt:
1,2 1 2 3 1 2
E : x - 2x + 2x = 20 und E : x - 2x + 2x = -10.
1 1 2 3 2 1 2 3
|
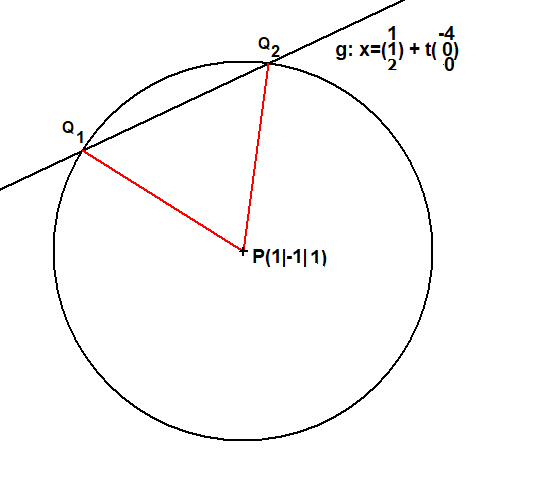 |
Bestimme die beiden Punkte Q1 und Q2
auf der Geraden g, die von P den Abstand 3 haben. |
-4t 2 2 2
|PQ|=|( 2 ) = 3 ist oder |PQ| =16t +4 + 1 = 9 ist, also 16t = 4
1
1 1
und damit t =— ⇒ Q (0|1|2) und t =-— ⇒ Q (2|1|2)
1 4 1 2 4 2
Lösung der 42. Lektion
Lösung der 1. Aufgabe:
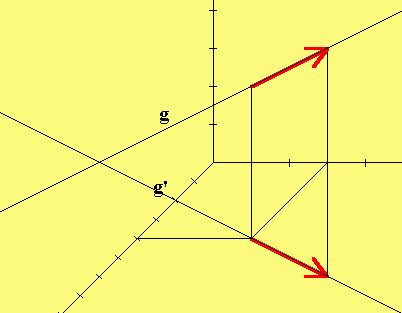
|
|4| |2| |4| |2|
-> | | | | -> | | | |
g: x = |3| + s|1| g': x = |3| + s|1|
| | | | | | | |
|4| |6| |0| |0|
Bei der Projektion wird x = 0.
3
Die Geraden kann man mit dem Aufpunkt
P (4|3|4) bzw. P'(4|3|0)
0 0
und einem weiteren Punkt zeichnen
z.B. P(4+2|3+1|4+6) bzw. P'(6|4|0).
|
Lösung der 2. Aufgabe:
|5| |1|
-> | | | |
Um die Projektion die Gerade g: x = |5| + s|1|
| | | |
|4| |4|
auf die Ebene E: x + x + x = 5 zu finden, projizieren
1 2 3
wir die Punkte P (5|5|4) und P (6|6|8) auf E.
0 1
Dazu bestimmen wir die Schnittpunkt Q und Q der Geraden
0 1
senkrecht zu E durch die Punkte mit E (siehe hier).
Wir erhalten Q (1|1|3) und Q (2|2|1). Somit ist die Projektion
0 1
|1| |1|
-> | | | |
von g auf E: g': x = |1| + s·|1|.
| | | |
|3| |2|
Lösung der 43. Lektion
Als ersten stellen wir fest: Die Geraden sind nicht
parallel und haben einen Schnittpunkt. Sie besitzen also
zwei winkelhalbierende Geraden.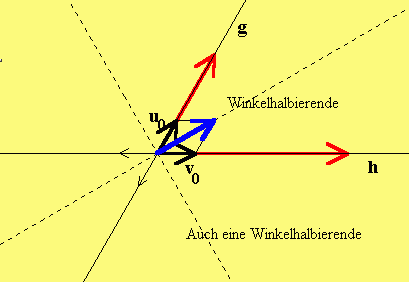
|
Wir ersetzten die Richtungsvektore der Geraden durch
Einheitsvektoren (Vektoren vom Betrag 1).
|2| |3|
-> 1 | | -> 1 | |
Einheitsrichtungsvektor von g u = -·|1| und von h v = -·|4|
0 3 | | 5 | |
|2| |0|
-> ->
Die Richtungsvektoren der Winkelhalbierenden sind dann u ± v .
0 0
Um Brüche zu vermeiden nehmen wir das 15-fache dieser Vektoren.
|10| | 9|
-> -> | | | |
15·(u ± v ) = | 5| ± |12|
0 0 | | | |
|10| | 0|
Die Gleichungen der winkelhalbierenden Geraden lauten dann:
|5| |19| |5| | 1|
-> | | | | -> | | | |
w : x = |5| + s|17| und h: x = |5| + s|-7|
1 | | | | | | | |
|5| |10| |5| |10|
Man beachte: Die Winkelhalbierenden stehen senkrecht aufeinander.
|
Lösung der 44. Lektion
Als ersten stellen wir fest: Die Ebenen sind nicht parallel und haben eine Schnittgerade. Sie besitzen also zwei winkelhalbierende Ebenen.Wir ersetzten ähnlich wie in Lektion 43 die Normalenvektoren der Ebenen durch Einheitsvektoren.
|2| |3|
-> 1 | | -> 1 | |
Die Einheitsnormalevektoren sind n = -·|1| und n = -·|4|
1 3 | | 2 5 | |
|2| |0|
-> ->
Die Normalenvektoren der Winkelhalbierenden sind dann n ± n
1 2
Um Brüche zu vermeiden nehmen wir das 15-fache dieser
Vektoren.Die winkelhalbierenden Ebenen sind dann:
W : 19x + 17x + 10x = d und W : x - 7x + 10x = d 1 1 2 3 1 2 1 2 3 2Für die Unbekannten d1,2 benötigen wir noch einen gemeinsamen Punkt von E1 und E2. Dazu gehen wir folgendermaßen vor:
Bei der Berechnung der Schnittgerade suchten wir eine allgemeine Lösung, hier genügt eine beliebige Lösung des folgenden LGS:
|2x + x + 2x = 0| Eine Lösung ist zum Beispiel | 1 2 3 | | | x = 0 => x = 2 => x = -2 |3x + 4x = 6| 2 1 3 | 1 2 |Ein Punkt der Schnittgeraden ist mit P(2|0|-2) gefunden. Er liegt auch auf den Winkelhalbierenden. Durch Punktprobe erhalten wir dann die rechte Seite der folgenden Gleichungen der Winkelhalbierenden:
W : 19x + 17x + 10x = 18 und W : x - 7x + 10x = -18 1 1 2 3 2 1 2 3Alternative Rechnung: Alle Punkte P(x1|x2|x3) haben von E1 und E2 gleichen Abstand: Diesen berechnen wir mit der Hesse-Form.
|2x + x + 2x | |3x + 4x - 6| | 1 2 3| | 1 2 | |————————————| = |———————————| . | 3 | | 5 |Ohne Betragsstriche geschrieben, dann aber die Gleichung mit "±" erhalten wir auch die Gleichungen für W1,2
Lösungen der 51. Lektion
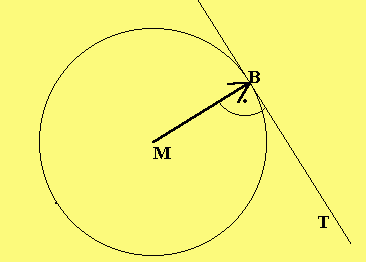
|
Lösung der 1. Aufgabe:Als erstes war zu zeigen: B(3|0|4) ist ein Punkt der Kugel mit Mittelpunkt M(1|-2|3) und Radius r = 3 LE:.
|2|
——> | |
|MB |= ||2|| = 3 = r => B liegt auf der Kugel.
| |
|1|
Als zweites war die Tangentengleichung in B an die Kugel zu
bestimmen:
——>
Die Tangente T hat MB als Normalenvektor
und geht durch B(3|0|4) => T: 2x + 2x + x = 10.
1 2 3
|
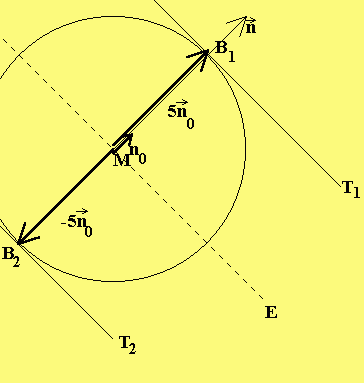
|
Lösung der 2. Aufgabe:Gegeben ist die Kugel mit Mittelpunkt M(-4|3|4) und Radius r = 5 LE und die Ebene
Die Berührpunkte sind 5 LE von M in Richtung des
|-6|
-> | |
Normalenvektors n = | 3| der Ebene E entfernt.
| |
| 2|
——> -> -> 1 ->
Also ist MB = ±5·n , wobei n = -·n
1,2 0 0 7
->
der Einheitsvektor von n ist.
2 1 3 2 6 4
Somit ist B (- 8-|5-|5-) und B (-|-|2-)
1 7 7 7 2 7 7 7
und die Tangenten T : -6x + 3x + 2x = 76
1 1 2 3
T : -6x + 3x + 2x = 6.
2 1 2 3
|
Lösungen der 52 Lektion
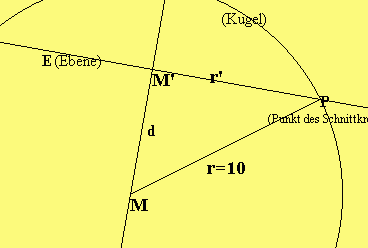
|
Die Ebene
|1| | 2|
-> | | | |
Die Gerade x = |1| + s·|-2| durch M senkrecht
| | | |
|1| | 1|
zu E schneidet die Ebene in M'(5|-3|3) (s=2).
Mit d = d(M,E) = 6 folgt nach Pythagoras
————————
r' = \/100 - 36 = 8 LE.
|